题目内容
已知a=
×100,问a的整数部分是
| 11×66+12×67+13×68+14×69+15×70 | 11×65+12×66+13×67+14×68+15×69 |
101
101
.分析:观察分数可以发现,分子首先拆成11×65+11+12×66+12+…15×69+15,把分子组合成两部分,可以化为1+一个小分数的形式,进一步利用乘法分配律展开,再据分子和分母的特点,再一次把分子拆分,直至讨论出最后结果.
解答:解:因为:a=
×100,
所以a=(1+
)×100,
=100+
,
=100+1+
,
这个分数的分子比分母小,小于1,所以a的整数部分是101.
故答案为:101.
| 11×66+12×67+13×68+14×69+15×70 |
| 11×65+12×66+13×67+14×68+15×69 |
所以a=(1+
| 11+12+…+15 |
| 11×65+12×66+…+15×69 |
=100+
| 11×100+12×100+…+15×100 |
| 11×65+12×66+??+15×69 |
=100+1+
| 11×35+12×34+…+15×31 |
| 11×65+12×66+…+15×69 |
| 11×35+12×34+…+15×31 |
| 11×65+12×66+…+15×69 |
故答案为:101.
点评:解答此题的关键要搞清分子与分母算式的贴点,灵活运用分数的拆项解决问题.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
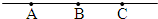 已知点A、B、C是直线上的三个点,则右面图中有
已知点A、B、C是直线上的三个点,则右面图中有