题目内容
甲、乙两个圆的半径比是2﹕3,甲圆面积是乙圆面积的
,乙圆周长比甲圆周长多
.
| ( ) |
| ( ) |
| ( ) |
| ( ) |
分析:根据“圆的周长=2πr”和“圆的面积=πr2”进行推导,进而得出结论.
解答:解:设小圆的半径为2r,则大圆的半径是3r,
甲圆面积是乙圆面积的:[π(2r)2]÷(π(3r)2),
=4πr2÷9πr2,
=
;
两个圆周长为:2π×2r=4πr,2π×3r=6πr
乙圆周长比甲圆周长多( 6πr-4πr)÷4πr=
.
故答案为:
,
.
甲圆面积是乙圆面积的:[π(2r)2]÷(π(3r)2),
=4πr2÷9πr2,
=
| 4 |
| 9 |
两个圆周长为:2π×2r=4πr,2π×3r=6πr
乙圆周长比甲圆周长多( 6πr-4πr)÷4πr=
| 1 |
| 2 |
故答案为:
| 4 |
| 9 |
| 1 |
| 2 |
点评:此题属于易错题,解答此题的关键是:灵活运用圆的周长计算方法和圆的面积计算公式,进行推导,进而得出结论.
注:两个圆的半径比,等于它的周长比,等于它直径的比;面积的比即半径平方的比.
注:两个圆的半径比,等于它的周长比,等于它直径的比;面积的比即半径平方的比.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
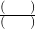 ,乙圆周长比甲圆周长多
,乙圆周长比甲圆周长多