题目内容
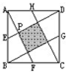 如图,EFGH分别是正方形ABCD各边上的中点,已知三角形AEP的面积是12平方厘米.求阴影部分的面积.
如图,EFGH分别是正方形ABCD各边上的中点,已知三角形AEP的面积是12平方厘米.求阴影部分的面积.
解:根据题干分析可得:
平行四边形AFCH的面积+平行四边形BGDE的面积=正方形ABCD的面积,
则两个平行四边形的面积和-阴影部分的面积+4×△AEP的面积=正方形ABCD的面积,
所以阴影部分的面积=4×三角形AEP的面积,
=4×12,
=48(平方厘米),
答:阴影部分的面积是48平方厘米.
分析: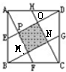 正方形中E、F、G、H分别是中点,在图形中,根据图形的平移和旋转的性质,可得出:△AEP、△BFM、△CGN、△DHO是形状、大小都相同的四个三角形;
正方形中E、F、G、H分别是中点,在图形中,根据图形的平移和旋转的性质,可得出:△AEP、△BFM、△CGN、△DHO是形状、大小都相同的四个三角形;
E、G分别是中点,可得:BE=DG,所以四边形BGDE是平行四边形,
同理,四边形AFCH也是平行四边形,
平行四边形AFCH的面积+平行四边形BGDE的面积=正方形ABCD的面积,
其中上式等式左边阴影部分的面积重合了一次,
则两个平行四边形的面积和-阴影部分的面积+4×△AEP的面积=正方形ABCD的面积,
所以阴影部分的面积=4×三角形AEP的面积=4×12=48(平方厘米),
点评:此题应用了平行四边形的定义以及平移与旋转的性质,将阴影部分的面积转化到平行四边形和三角形的面积中进行求解.
平行四边形AFCH的面积+平行四边形BGDE的面积=正方形ABCD的面积,
则两个平行四边形的面积和-阴影部分的面积+4×△AEP的面积=正方形ABCD的面积,
所以阴影部分的面积=4×三角形AEP的面积,
=4×12,
=48(平方厘米),
答:阴影部分的面积是48平方厘米.
分析:
 正方形中E、F、G、H分别是中点,在图形中,根据图形的平移和旋转的性质,可得出:△AEP、△BFM、△CGN、△DHO是形状、大小都相同的四个三角形;
正方形中E、F、G、H分别是中点,在图形中,根据图形的平移和旋转的性质,可得出:△AEP、△BFM、△CGN、△DHO是形状、大小都相同的四个三角形;E、G分别是中点,可得:BE=DG,所以四边形BGDE是平行四边形,
同理,四边形AFCH也是平行四边形,
平行四边形AFCH的面积+平行四边形BGDE的面积=正方形ABCD的面积,
其中上式等式左边阴影部分的面积重合了一次,
则两个平行四边形的面积和-阴影部分的面积+4×△AEP的面积=正方形ABCD的面积,
所以阴影部分的面积=4×三角形AEP的面积=4×12=48(平方厘米),
点评:此题应用了平行四边形的定义以及平移与旋转的性质,将阴影部分的面积转化到平行四边形和三角形的面积中进行求解.

练习册系列答案
相关题目
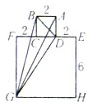 如图,正方形ABCD与正方形EFGH的边长分别是2厘米、6厘米,求△ADG和△BGD的面积.
如图,正方形ABCD与正方形EFGH的边长分别是2厘米、6厘米,求△ADG和△BGD的面积.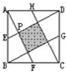 如图,EFGH分别是正方形ABCD各边上的中点,已知三角形AEP的面积是12平方厘米.求阴影部分的面积.
如图,EFGH分别是正方形ABCD各边上的中点,已知三角形AEP的面积是12平方厘米.求阴影部分的面积.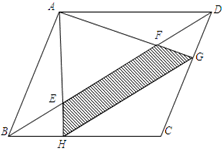 如图,平行四边形ABCD的面积为36平方厘米,H、G分别是 BC、CD边上靠近B和D的三等分点,四边形EFGH的面积为
如图,平行四边形ABCD的面积为36平方厘米,H、G分别是 BC、CD边上靠近B和D的三等分点,四边形EFGH的面积为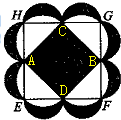 如图,阴影正方形的顶点分别是大正方形EFGH各边的中点,分别以大正方形各边的一半为直径向外作半圆,再分别以阴影正方形的各边为直径向外作半圆,形成8个“月牙形”.这8个“月牙形”的总面积为5平方厘米,问大正方形EFGH的面积是多少平方厘米?
如图,阴影正方形的顶点分别是大正方形EFGH各边的中点,分别以大正方形各边的一半为直径向外作半圆,再分别以阴影正方形的各边为直径向外作半圆,形成8个“月牙形”.这8个“月牙形”的总面积为5平方厘米,问大正方形EFGH的面积是多少平方厘米?