题目内容
在一个圆柱中挖去一个最大的圆锥,剩下部分的体积是挖去部分的________倍.
2
分析:把一个圆柱挖出一个最大的圆锥,则这个圆柱与圆锥等底等高,所以圆柱的体积是圆锥的体积的3倍,则剩下部分的体积与圆锥的体积的2倍,由此即可解答.
解答:根据题干分析可得:这个圆柱的体积与挖出的圆锥是等底等高,
所以圆柱的体积是圆锥的体积的3倍,
则剩下部分的体积是圆锥的体积的2倍;
故答案为:2.
点评:抓住圆柱内最大的圆锥的特点,利用等底等高的圆柱与圆锥的体积倍数关系即可解决此类问题.
分析:把一个圆柱挖出一个最大的圆锥,则这个圆柱与圆锥等底等高,所以圆柱的体积是圆锥的体积的3倍,则剩下部分的体积与圆锥的体积的2倍,由此即可解答.
解答:根据题干分析可得:这个圆柱的体积与挖出的圆锥是等底等高,
所以圆柱的体积是圆锥的体积的3倍,
则剩下部分的体积是圆锥的体积的2倍;
故答案为:2.
点评:抓住圆柱内最大的圆锥的特点,利用等底等高的圆柱与圆锥的体积倍数关系即可解决此类问题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 B.
B.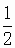 C.2倍 D.3倍
C.2倍 D.3倍