题目内容
 如图,长方形EFGH的长HE和宽EF分别是6cm和4cm,四边形ABCD的面积为1.8平方厘米,那么阴影部分的面积和为多少平方厘米?
如图,长方形EFGH的长HE和宽EF分别是6cm和4cm,四边形ABCD的面积为1.8平方厘米,那么阴影部分的面积和为多少平方厘米?
解: (6×4)-[
(6×4)-[ (6×4)-1.8],
(6×4)-1.8],
=12-(6-1.8),
=12-4.2,
=7.8(平方厘米);
答:阴影部分的面积是7.8平方厘米.
分析:根据题意可知△AGH和△AFE的面积和是长方形面积的一半,△HCE的面积是长方形面积的 .由于四边形ABCD的面积是1.8平方厘米,易求△ABH和△ADE的面积和,从而求出四边形ABCD的面积.
.由于四边形ABCD的面积是1.8平方厘米,易求△ABH和△ADE的面积和,从而求出四边形ABCD的面积.
点评:考查了组合图形的面积,本题的难点是理解四边形ABCD的面积=△HCE的面积-(△ABH和△ADE的面积和),以及△AGH和△AFE的面积和、△HCE的面积与长方形面积的关系.
 (6×4)-[
(6×4)-[ (6×4)-1.8],
(6×4)-1.8],=12-(6-1.8),
=12-4.2,
=7.8(平方厘米);
答:阴影部分的面积是7.8平方厘米.
分析:根据题意可知△AGH和△AFE的面积和是长方形面积的一半,△HCE的面积是长方形面积的
 .由于四边形ABCD的面积是1.8平方厘米,易求△ABH和△ADE的面积和,从而求出四边形ABCD的面积.
.由于四边形ABCD的面积是1.8平方厘米,易求△ABH和△ADE的面积和,从而求出四边形ABCD的面积.点评:考查了组合图形的面积,本题的难点是理解四边形ABCD的面积=△HCE的面积-(△ABH和△ADE的面积和),以及△AGH和△AFE的面积和、△HCE的面积与长方形面积的关系.

练习册系列答案
相关题目
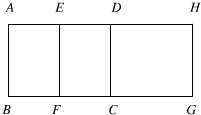 如图,长方形ABCD的面积是2l平方厘米,长方形EFGH的面积是24平方厘米,它们的宽都是3厘米,线段AH长为13厘米,则四边形CDEF的面积
如图,长方形ABCD的面积是2l平方厘米,长方形EFGH的面积是24平方厘米,它们的宽都是3厘米,线段AH长为13厘米,则四边形CDEF的面积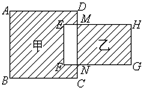 如图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是
如图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是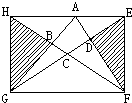 如图,长方形EFGH的长HE和宽EF分别是6cm和4cm,四边形ABCD的面积为1.8平方厘米,那么阴影部分的面积和为多少平方厘米?
如图,长方形EFGH的长HE和宽EF分别是6cm和4cm,四边形ABCD的面积为1.8平方厘米,那么阴影部分的面积和为多少平方厘米?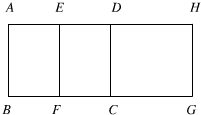 如图,长方形ABCD的面积是2l平方厘米,长方形EFGH的面积是24平方厘米,它们的宽都是3厘米,线段AH长为13厘米,则四边形CDEF的面积________.
如图,长方形ABCD的面积是2l平方厘米,长方形EFGH的面积是24平方厘米,它们的宽都是3厘米,线段AH长为13厘米,则四边形CDEF的面积________.