题目内容
两条平行线上各有n个点,用这n对点按如下规则连接线段: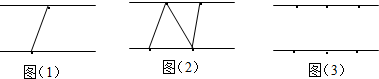
①平行线之间的点在连线段时,可以有共同的端点,但不能有其他交点;
②符合①要求的线段必须全部画出;
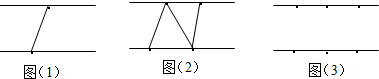
图(1)展示了当n=1时的情况,此时图中三角形的个数为0;
图(2)展示了当n=2时的情况,此时图中三角形的个数为2;
(1)当n=3时,请在图(3)中画出使三角形个数最少的图形,此时图中三角形的个数为________;
(2)当n=2012时,按上述规则画出的图形中,最少有________个三角形.
解:(1)
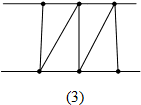
此时图中三角形的个数是:4个;
据此分析可得:当有n对点时,最少可以画2(n-1)个三角形;
(2)当n=2012时,2×(2012-1)=4022(个).
答:当n=2012时,最少可以画4022个三角形.
故答案为:4;4022.
分析:(1)根据题意画出图形,根据图形数出三角形个数即可得出答案;据此分析可得,当n=1时的情况,此时图中三角形的个数为0,有0=2(1-1);当n=2时的一种情况,此时图中三角形的个数为2,有2=2(2-1);…故当有n对点时,最少可以画2(n-1)个三角形;
(2)当n=2012时,按上述规则画出的图形中,最少有2×(2012-1)=4022个三角形.
点评:此题考查了图形的规律变化,要求学生通过观察图形,分析、归纳发现其中的规律,并应用规律解决问题.

此时图中三角形的个数是:4个;
据此分析可得:当有n对点时,最少可以画2(n-1)个三角形;
(2)当n=2012时,2×(2012-1)=4022(个).
答:当n=2012时,最少可以画4022个三角形.
故答案为:4;4022.
分析:(1)根据题意画出图形,根据图形数出三角形个数即可得出答案;据此分析可得,当n=1时的情况,此时图中三角形的个数为0,有0=2(1-1);当n=2时的一种情况,此时图中三角形的个数为2,有2=2(2-1);…故当有n对点时,最少可以画2(n-1)个三角形;
(2)当n=2012时,按上述规则画出的图形中,最少有2×(2012-1)=4022个三角形.
点评:此题考查了图形的规律变化,要求学生通过观察图形,分析、归纳发现其中的规律,并应用规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目