题目内容
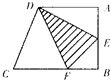 如图,ABCD是直角梯形,其中AD=12厘米,AB=8厘米,BC=15厘米,且△ADE、四边形DEBF、△CDF的面积相等.△EDF(阴影部分)的面积是多少平方厘米?
如图,ABCD是直角梯形,其中AD=12厘米,AB=8厘米,BC=15厘米,且△ADE、四边形DEBF、△CDF的面积相等.△EDF(阴影部分)的面积是多少平方厘米?
解:S梯形=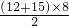 ,
,
=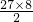 ,
,
=108(平方厘米);
 ,
,
AE=36×2÷12,
=72÷12,
=6(厘米),
BE=8-6=2(厘米),
CF=36×2÷8,
=72÷8,
=9(厘米),
BF=15-9=6(厘米),
所以S△EBF=6×2÷2=6(平方厘米),
阴影部分的面积=36-6=30(平方厘米).
答:阴影部分的面积是30平方厘米.
分析:由题意可知:梯形的面积可求,则S四边形DEBF、S△ADE、S△DCF可求,从而可以求出AE、BE,S△CDF可求,则CF、BF可求,从而可以求出S△EBF,阴影部分的面积=S四边形DEBF-S△EBF,问题得解.
点评:解答此题的关键是利用等量代换,将阴影部分利用其他图形的面积转化出来.
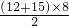 ,
,=
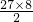 ,
,=108(平方厘米);
 ,
,AE=36×2÷12,
=72÷12,
=6(厘米),
BE=8-6=2(厘米),
CF=36×2÷8,
=72÷8,
=9(厘米),
BF=15-9=6(厘米),
所以S△EBF=6×2÷2=6(平方厘米),
阴影部分的面积=36-6=30(平方厘米).
答:阴影部分的面积是30平方厘米.
分析:由题意可知:梯形的面积可求,则S四边形DEBF、S△ADE、S△DCF可求,从而可以求出AE、BE,S△CDF可求,则CF、BF可求,从而可以求出S△EBF,阴影部分的面积=S四边形DEBF-S△EBF,问题得解.
点评:解答此题的关键是利用等量代换,将阴影部分利用其他图形的面积转化出来.

练习册系列答案
相关题目
 (2009?崇文区)如图,ABCD是直角梯形,已知OE垂直于DC,AD=10厘米,三角形BOC面积为15平方厘米,那么三角形ADO的面积是
(2009?崇文区)如图,ABCD是直角梯形,已知OE垂直于DC,AD=10厘米,三角形BOC面积为15平方厘米,那么三角形ADO的面积是 如图,ABCD是直角梯形,AD=5厘米,DC=3厘米,三角形DOC的面积是1.5平方厘米,则阴影部分的面积是
如图,ABCD是直角梯形,AD=5厘米,DC=3厘米,三角形DOC的面积是1.5平方厘米,则阴影部分的面积是 如图,ABCD是直角梯形,AEFC是长方形,已知BC-AD=6厘米,CD=8厘米,梯形面积是80平厘米.求阴影部分的面积.
如图,ABCD是直角梯形,AEFC是长方形,已知BC-AD=6厘米,CD=8厘米,梯形面积是80平厘米.求阴影部分的面积. 如图,ABCD是直角梯形,以CD为轴并将梯形绕这个轴旋转一周,得到一个立体图形,它的体积是多少立方厘米?
如图,ABCD是直角梯形,以CD为轴并将梯形绕这个轴旋转一周,得到一个立体图形,它的体积是多少立方厘米? 如图,ABCD是直角梯形,上底AD是12厘米,高CD是7.2厘米,阴影部分的面积是7.2平方厘米,求梯形ABCD的面积.
如图,ABCD是直角梯形,上底AD是12厘米,高CD是7.2厘米,阴影部分的面积是7.2平方厘米,求梯形ABCD的面积.