题目内容
【题目】(扬州)学校食堂有一个底面直径是60厘米,高80厘米的圆柱形水箱,水箱中装有A、B两个进水管,先开A管,过一段时间后两管同开,下面折线图表示进水情况,请根据图回答以下问题.
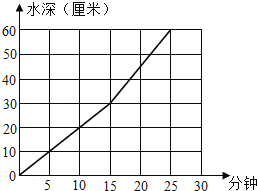
(1)A管开放多少分钟后,B管开始与A管同时进水?
(2)A管12分钟进水多少升?
(3)A、B两管同时进水,每分钟进水多少升?
【答案】(1)A管开放15分钟后,B管开始与A管同时进水;(2)A管12分钟进水67.824升
【解析】
试题分析:(1)折线与横轴的角度变大时说明B进水管打开了;
(2)先求出水深,根据圆柱的体积公式,求出此时水的体积;
(3)先分别求出这两个水管的每分钟共进水多少厘米,再根据圆柱的体积公式,求出此时水的体积;(3)A、B两管同时进水,每分钟进水8.478升
解答:解:(1)15分钟时折线与横轴的角度变大,此时打开了B进水管.
答:A管开放15分钟后,B管开始与A管同时进水.
(2)12分钟时水深为:
10÷5×12=24(厘米)
此时水的体积为:
3.14×![]() ×24
×24
=3.14×900×24
=67824(立方厘米)
=67.824(升);
答:A管12分钟进水67.824升.
(3)同时开1分钟的进水深度为:
(60﹣30)÷(25﹣15)
=30÷10
=3(厘米)
此时水的体积为:
3.14×![]() ×3
×3
=3.14×900×3
=8478(立方厘米)
=8.478(升)
答:A、B两管同时进水,每分钟进水8.478升.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目