题目内容
如图,大正方形的边长为8厘米,求阴影部分的周长和面积.(结果保留π)


分析:由题意可知:阴影部分的周长=圆的周长的
×2+正方形的边长的
×4,据此代入数据即可求解;
将左下角圆以外的阴影部分挪到左上角,则阴影部分的面积=正方形的面积的一半+圆的面积的一半,据此利用正方形和圆的面积公式即可求解.
| 1 |
| 4 |
| 1 |
| 2 |
将左下角圆以外的阴影部分挪到左上角,则阴影部分的面积=正方形的面积的一半+圆的面积的一半,据此利用正方形和圆的面积公式即可求解.
解答:解:周长:π×8×
×2+8×
×4
=8π×
+16
=4π+16(厘米);
面积:8×8×
+π×(8÷2)2×
=32+8π(平方厘米).
答:阴影部分的周长是4π+16厘米,面积是32+8π平方厘米.
| 1 |
| 4 |
| 1 |
| 2 |
=8π×
| 1 |
| 2 |
=4π+16(厘米);
面积:8×8×
| 1 |
| 2 |
| 1 |
| 2 |
=32+8π(平方厘米).
答:阴影部分的周长是4π+16厘米,面积是32+8π平方厘米.
点评:解答此题的关键是弄清楚:阴影部分的周长由哪些线段或曲线组成;阴影部分的面积可以由哪些图形的面积和或差求解,从而问题得解.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图,大正方形的边长是5厘米,阴影部分的面积是
如图,大正方形的边长是5厘米,阴影部分的面积是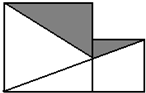 如图,大正方形的边长是10分米,小正方形的边长是6分米,求阴影部分面积.
如图,大正方形的边长是10分米,小正方形的边长是6分米,求阴影部分面积.
 如图,大正方形的边长为1,
如图,大正方形的边长为1,