题目内容
18.一个正方形的边长增加$\frac{1}{8}$,它的周长将增加$\frac{()}{()}$,面积增加$\frac{()}{()}$.分析 如图所示,设正方形的边长为a,则新正方形的边长为(a+$\frac{1}{8}$a),而增加的部分由两个相同的长方形(长为a、宽为 $\frac{1}{8}$a)和一个边长为 $\frac{1}{8}$a的正方形周长,从而利用正方形的周长面积公式求出问题的答案.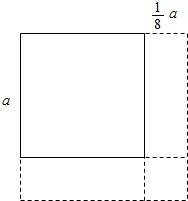
解答 解:设正方形的边长为a,则新正方形的边长为(a+$\frac{1}{8}$%a),
新正方形的面积增加了:$\frac{1}{8}$a2×2+${(\frac{1}{8}a)}^{2}$
=$\frac{1}{8}$a2+$\frac{1}{64}$a2
=$\frac{9}{64}$a2
$\frac{9}{64}$a2÷a2=$\frac{9}{64}$;
新正方形比原正方形的周长增加了:4×$\frac{1}{8}$a=$\frac{1}{2}$ a,
$\frac{1}{2}$a÷4a=$\frac{1}{8}$;
故答案为:$\frac{1}{8}$、$\frac{9}{64}$.
点评 解答此题的关键是弄清楚变化后的图形由哪些部分组成,从而可以求出周长和面积的变化情况.

练习册系列答案
相关题目
8.表是四(3)班学生一次英语测试成绩(单位:分)
(1)根据上面的数据填写表.
(2)全班总分数是1700分,参加考试的有20人,90至99分数段的人数最多.
(3)最高分是100分,最低分是55分,平均分是85分.
| 姓名 | 成绩 | 姓名 | 成绩 | 姓名 | 成绩 | 姓名 | 成绩 |
| 毛悦 | 84 | 徐明 | 91 | 刘茜 | 98 | 吴泽 | 100 |
| 王星星 | 79 | 赵琳 | 86 | 尤立 | 97 | 刘俊斌 | 69 |
| 曹伟 | 86 | 单波 | 95 | 许亚迪 | 94 | 张悦 | 59 |
| 李一波 | 93 | 冯小宁 | 85 | 王小青 | 96 | 张文军 | 77 |
| 顾洁 | 100 | 花小波 | 55 | 朱小林 | 82 | 高源 | 74 |
| 分数(分) | 60分以下 | 60~69 | 70~79 | 80~89 | 90~99 | 100 |
| 人数(人) |
(3)最高分是100分,最低分是55分,平均分是85分.
13.化简下面各比,并求出比值.
| 比 | 35:14 | 0.9:1.35 | 2:$\frac{2}{13}$ | $\frac{3}{8}$:$\frac{1}{4}$ |
| 最简整数比 | ||||
| 比值 |
2.
| 2米-3分米=17分米; | 32厘米+68厘米=10分米; |
| 语文课本约厚1厘米,相当于10毫米; | 6吨=6000千克; |
| 5千米+1000米=6千米; | 8000千克-2吨=6吨. |