题目内容
16. 如图是一个长5厘米、宽3厘米的长方形.
如图是一个长5厘米、宽3厘米的长方形.(1)在长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形.
(2)求直角三角形的面积.
(3)以等腰直角三角形的一个直角边所在的直线为轴,将三角形旋转,可以形成圆锥.算出旋转形成的这个图形的体积.(得数保留两位小数)
分析 (1)从长的5厘米中量出3厘米的点,再与下角画一条线段,就成一个等腰直角三角形和一个梯形;
(2)将数据代入三角形面积公式:三角形面积=底×高÷2,即可求出三角形的面积;
(3)等腰三角形高速旋转得到圆锥,此圆锥的底面半径和高都等于三角形的直角边,将数据代入圆锥的体积公式V=$\frac{1}{3}$Sh即可求其体积.
解答 解:(1)所作的等腰直角三角形的直角边是3厘米,梯形的上底是5-3=2厘米,下底是5厘米,高是3厘米;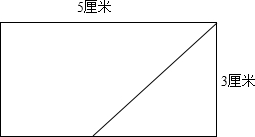
(2)3×3÷2=4.5(平方厘米)
答:直角三角形的面积是4.5平方厘米;
(3)以等腰直角三角形的一个直角边所在的直线为轴,将三角形高速旋转,可以形成圆锥形,
圆锥的体积:
$\frac{1}{3}$×3.14×32×3
=3.14×9
=28.26(立方厘米)
答:将三角形旋转,可以形成圆锥.旋转形成的这个图形的体积是28.26立方厘米.
故答案为:圆锥.
点评 此题主要考查图形划分、三角形面积公式及圆锥的体积公式,关键是找清圆锥下底的半径和高,将数据代入公式即可求得结果.

练习册系列答案
相关题目
