题目内容
6.画一个周长是12.56厘米的圆,然后在圆内画一个最大的正方形,并求出正方形的面积是圆面积的几分之几?分析 (1)先确定圆心,以(12.56÷3.14÷2)厘米长为半径画圆即可,再利用圆的面积=πr2即可求出圆的面积;在圆中所画最大正方形的对角线应该等于圆的直径,从而利用对角线×对角线÷2可以求出这个正方形的面积.
(2)根据题意可知:这个圆的直径就是正方形的边长,再依据圆的面积公式:s=πr2即可求其面积,再利用正方形的面积除以圆的面积即可解答问题.
解答 解:12.56÷3.14÷2=2(厘米)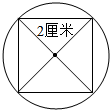
所以圆的面积是:3.14×22=12.56(平方厘米)
正方形的面积是:(2×2)×(2×2)÷2=8(平方厘米)
正方形的面积是圆面积的:8÷12.56=$\frac{100}{157}$
答:正方形的面积是圆面积的$\frac{100}{157}$.
点评 此题考查了圆的画法.抓住圆的两大要素:圆心和半径.即可解决此类问题.第二问的关键是明白:最大正方形的对角线应该等于圆的直径,从而逐步求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.假分数与它的倒数进行比较,结果是( )
| A. | 假分数小于它的倒数 | B. | 假分数大于它的倒数 | ||
| C. | 假分数小于或等于它的倒数 | D. | 假分数大于或等于它的倒数 |