题目内容
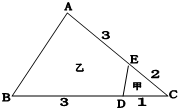如图中的三角形被分成了甲、乙两部分，甲、乙两部分的面积之比是多少？（单位：厘米）
解：
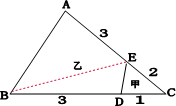
连接BE，根据分析知：
△BDE与△DCE的面积的比为3：1，
△ABE与△BCE面积的比为3：2，
设△DCE的面积为x，△BDE的面积就是3x，则△BCE的面积是：
3x+4x=4x，
△ABE的面积是：
4x×
=6x，
S甲：S乙=（S△ABE+S△BDE）：S△DCE=（6x+3x）：x=9x：x=9：1．
答：甲、乙两部分的面积之比是9：1．
分析：边接BE，△BDE与△DCE的高相同，面积的比就是底的比为3：1，△ABE与△BCE的高相同，它们面积的比就是底的比既3：2，设△DCE的面积是x，则△BDE的面积是3x，则△BCE的面积是4x，据此可求出△ABE的面积为多少．据此解答．
点评：本题的关键是连接BE，然后再根据等高的三角形的面积比就等于底的比的关系，进行解答．
连接BE，根据分析知：
△BDE与△DCE的面积的比为3：1，
△ABE与△BCE面积的比为3：2，
设△DCE的面积为x，△BDE的面积就是3x，则△BCE的面积是：
3x+4x=4x，
△ABE的面积是：
4x×
=6x，S甲：S乙=（S△ABE+S△BDE）：S△DCE=（6x+3x）：x=9x：x=9：1．
答：甲、乙两部分的面积之比是9：1．
分析：边接BE，△BDE与△DCE的高相同，面积的比就是底的比为3：1，△ABE与△BCE的高相同，它们面积的比就是底的比既3：2，设△DCE的面积是x，则△BDE的面积是3x，则△BCE的面积是4x，据此可求出△ABE的面积为多少．据此解答．
点评：本题的关键是连接BE，然后再根据等高的三角形的面积比就等于底的比的关系，进行解答．
练习册系列答案
相关题目
如图，长方形ABCD被分成两个长方形，且AB：AE=4：1，图中阴影部分三角形的面积为2平方分米．则长方形ABCD的面积为（ ）
如图中的三角形被分成了甲、乙两部分，甲、乙两部分的面积之比是多少？（单位：厘米）
如图中的三角形ABC被分成了阴影、空白两部分，D是BC的中点，E是AB的三等分点，求阴影部分面积是空白部分面积的几分之几？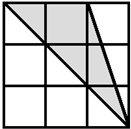
（2013?广州模拟）如图中的正方形被分成9个相同的小正方形，它们共有16个顶点（共同的顶点算一个）．以其中不在一条直线上的3个点为顶点，可连成三角形．在这些三角形中，与阴影三角形面积相等（包括它本身）的有