题目内容
下面等式中，相同字母表示同一数字，不同字母表示不同的数字：若
÷
=
，那么
=
. |
| 5EBBC6 |
. |
| DE |
. |
| DEE3 |
. |
| EBBC |
2005
2005
．分析：本题根据已知先推出E=2，再根据数的规律推知B=0，C=5，D=7．本题得以解答．
解答：解：因为5EBBC6÷DE=DEE3，
由6÷E=3可知E=2，所以原式变为：52BBC6÷D2=D223，
因为被除数是六位数，除数是两位数，商是四位数．可推知D＞5．D可能等于6、7、8或9．
当D=6、8或9时，经验算不合适．所以D=7．
原式为52BBC6÷72=7223，因此被除数为：7223×72=520056；
所以：B=0，C=5，因此原式为520056÷72=7223；
所以EBBC=2005．
故答案为：2005．
由6÷E=3可知E=2，所以原式变为：52BBC6÷D2=D223，
因为被除数是六位数，除数是两位数，商是四位数．可推知D＞5．D可能等于6、7、8或9．
当D=6、8或9时，经验算不合适．所以D=7．
原式为52BBC6÷72=7223，因此被除数为：7223×72=520056；
所以：B=0，C=5，因此原式为520056÷72=7223；
所以EBBC=2005．
故答案为：2005．
点评：此题考查数的整除及推理能力，比较繁琐．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
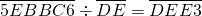，那么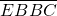
=________．