题目内容
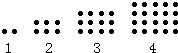 观察点阵,想想,第10个点阵中有________个点.
观察点阵,想想,第10个点阵中有________个点.
110
分析:观察图形可得:第一幅图中有2个点,可以写成12+1;第二幅图中有6个点,可以写成22+2;第三幅图中有12个点,可以写成32+3;第四幅图中有20个点,可以写成42+4…,由此可得第n幅图中的点数为:n2+n.
解答:根据题干分析可得每个图中的点数个数的规律是:第n幅图中的点数为:n2+n;
当n=10时,点阵中的点数为:102+10=110(个);
答:第10个点阵中有110个点.
故答案为:110.
点评:解决此类问题的关键是:根据题干中的图形找出事物排列的一般规律,从而即可解答.
分析:观察图形可得:第一幅图中有2个点,可以写成12+1;第二幅图中有6个点,可以写成22+2;第三幅图中有12个点,可以写成32+3;第四幅图中有20个点,可以写成42+4…,由此可得第n幅图中的点数为:n2+n.
解答:根据题干分析可得每个图中的点数个数的规律是:第n幅图中的点数为:n2+n;
当n=10时,点阵中的点数为:102+10=110(个);
答:第10个点阵中有110个点.
故答案为:110.
点评:解决此类问题的关键是:根据题干中的图形找出事物排列的一般规律,从而即可解答.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 观察点阵,想想,第10个点阵中有
观察点阵,想想,第10个点阵中有