题目内容
 小实践.在如图所示空框中,先画一条线段,把它分成一个最大的等腰直角三角形和一个梯形.再量一量有关数据,算出梯形的面积.
小实践.在如图所示空框中,先画一条线段,把它分成一个最大的等腰直角三角形和一个梯形.再量一量有关数据,算出梯形的面积.分析:要使分的等腰直角三角形最大,就要用这个长方形的宽作为等腰直角三角形的直角边.据此作画图,然后量出这个梯形的上底,下底和高,再根据梯形的面积公式求出它的面积.据此解答.
解答:解:根据分析画图如下:
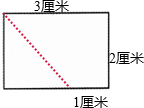
梯形的面积是:
S=(a+b)h÷2,
=(1+3)×2÷2,
=4×2÷2,
=4(平方厘米).
答:这个梯形的面积是4平方厘米.

梯形的面积是:
S=(a+b)h÷2,
=(1+3)×2÷2,
=4×2÷2,
=4(平方厘米).
答:这个梯形的面积是4平方厘米.
点评:本题综合考查了学生划分图形,及测量计算的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目