Question

在右面正方形ABCD内添上虚线，并在图外用文字说明，使它表示等式(a+b)2=a2

+2ab+b

2

．
说明：

一方面，大正方形的边长是a+b，面积=（a+b）²．另一方面，大正方形的面积等于两个小正方形的面积与两个小长方形的面积之和，为a²+2ab+b²，即（a+b）²=a²+2ab+b²

．

Answer 1

分析：图中大正方形的面积可以用正方形的面积公式来求，也可把正方形分成四个小图形分别求出面积再相加，从而得出（a+b）²=a²+2ab+b²；

解答：解：如图所示：

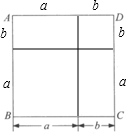
一方面，大正方形的边长是a+b，面积=（a+b）²．另一方面，大正方形的面积等于两个小正方形的面积与两个小长方形的面积之和，为a²+2ab+b²，即（a+b）²=a²+2ab+b²．

点评：本题考查了完全平方公式的几何意义，是对（a+b+c）²=a²+b²+c²+2ab+2bc+2ac的几何证明．