题目内容
(2013?吴中区)将一些数字分别填入下列各表中,要求每个小格中填入一个数字,表中的每横行中从左到右数字由小到大,每一数列中从上到下数字也由小到大排列.
(1)将1至4填入表1中,方法有
(2)将1至6填入表2中,方法有
(3)将1至9填入表3中,方法有
表1:
表2:
表3:
(1)将1至4填入表1中,方法有
2
2
种;(2)将1至6填入表2中,方法有
5
5
种;(3)将1至9填入表3中,方法有
42
42
种;表1:
分析:(1)要符合每横行从左到右数字由小到大,每竖列从上到下数字也由小到大排列.图一中,1只能在A的位置,4只能在D的位置,2和3可在B、C这两个格子中排列,所以共有2种方法;
(2)图二中,1只能在A的位置,6只能在F的位置,2只能在B和D,5只能在C、E的位置,数字5在C,有2种排列,数字5在E,又有3种排列方法;所以一共有2+3=5(种).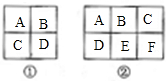
(3)由(2)的规律已经知道,6格是5种,1、2、3确定后,剩下的6个一定是5种;由此进行求解.
(2)图二中,1只能在A的位置,6只能在F的位置,2只能在B和D,5只能在C、E的位置,数字5在C,有2种排列,数字5在E,又有3种排列方法;所以一共有2+3=5(种).

(3)由(2)的规律已经知道,6格是5种,1、2、3确定后,剩下的6个一定是5种;由此进行求解.
解答:解:(1)如图,1和4是固定的,另外两格随便选,2种.
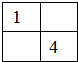
如下:
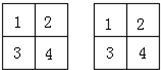 ;
;
(2)1和6是固定的,其余的不确定:

(3)由(2)的规律已经知道,6格是5种;
1、2、3确定后,剩下的6个一定是5种,比如:

同理:
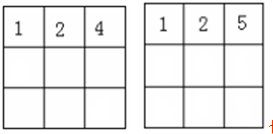 也对各对应5个;
也对各对应5个;
但是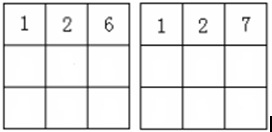 例外,对应的不是5个.因为第一排右边的数限制了下面的数.
例外,对应的不是5个.因为第一排右边的数限制了下面的数.
如下:
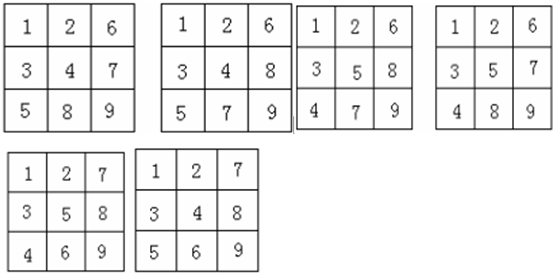
所以:共计5+5+5+4+2=21( )种)
同理,以上所有情况倒过来后都有一一对应的种类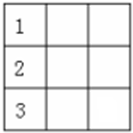
翻了一番,共21×2=42(种).
故答案为:2,5,42.

如下:
 ;
;(2)1和6是固定的,其余的不确定:

(3)由(2)的规律已经知道,6格是5种;
1、2、3确定后,剩下的6个一定是5种,比如:

同理:
 也对各对应5个;
也对各对应5个;但是
 例外,对应的不是5个.因为第一排右边的数限制了下面的数.
例外,对应的不是5个.因为第一排右边的数限制了下面的数.如下:

所以:共计5+5+5+4+2=21( )种)
同理,以上所有情况倒过来后都有一一对应的种类

翻了一番,共21×2=42(种).
故答案为:2,5,42.
点评:本题关键是根据题干的要求先确定出最大和最小的数字的位置.数字问题是排列计数原理中的一大类问题,条件变换多样,把排列问题包含在数字问题中,解题的关键是看清题目的实质,很多题目要分类讨论,要做到不重不漏.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目