题目内容
1.如图:在直角三角形ABC中,两直角边BC=5cm,AB=4cm,求图中阴影部分面积?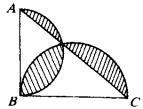
分析 可以按照如下进行分割: ,通过图形知S阴影部分面积=S半圆AB的面积+S半圆BC的面积-S△ABC的面积,所以由圆的面积公式和三角形的面积公式可以求得阴影部分的面积,列式解答即可.
,通过图形知S阴影部分面积=S半圆AB的面积+S半圆BC的面积-S△ABC的面积,所以由圆的面积公式和三角形的面积公式可以求得阴影部分的面积,列式解答即可.
解答 解:S阴影部分面积=S半圆AB的面积+S半圆BC的面积-S△ABC的面积
=3.14×(4÷2)2÷2+3.14×(5÷2)2÷2-5×4÷2
=3.14×4÷2+3.14×6.25÷2-20÷2
=6.28+9.8125-10
=16.0925-10
=6.0925(平方厘米)
答:图中阴影部分面积6.0925平方厘米.
点评 关键是弄清楚组合图形的面积可以由哪些我们学过的图形的面积的和或差求出.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 将1.8L水倒入如图中两个长方体水槽中,使它们的水面高度相等,这个高度是多少?(单位:厘米)
将1.8L水倒入如图中两个长方体水槽中,使它们的水面高度相等,这个高度是多少?(单位:厘米)