题目内容
当两个完全相同的长方形可以拼成一个正方形时，每个长方形的长一定是
宽的2倍
宽的2倍
．分析：当两个完全相同的长方形可以拼成一个正方形时，是把两个长方形的一条边对在一起，拼成正方形的边长就是长方形的长，也是2个宽的长度，由此求解．
解答：解：当两个完全相同的长方形可以拼成一个正方形，如图：
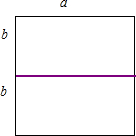
拼成的正方形的边长是原来长方形的长a，也是原来长方形的两个宽2b；
由此可得：长方形的长是长方形宽的2倍．
故答案为：宽的2倍．
拼成的正方形的边长是原来长方形的长a，也是原来长方形的两个宽2b；
由此可得：长方形的长是长方形宽的2倍．
故答案为：宽的2倍．
点评：本题关键是找出拼组的方法，通过拼成的正方形的边长与原来长方形的长和宽的关系进行推算求解．
练习册系列答案
相关题目
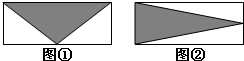两个完全相同的长方形（如图），将图①和图②阴影部分的面积相比，（ ）
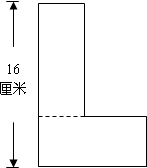如图，周长为52厘米的“L”形纸片可沿虚线分成两个完全相同的长方形．如果最长的边长是16厘米，那么该“L”形纸片的面积是
如图，周长为52厘米的“L”形纸片可沿虚线分成两个完全相同的长方形．如果最长的边长是16厘米，那么该“L”形纸片的面积是________平方厘米．