题目内容
 ABCD为任意四边形,其中AE=
ABCD为任意四边形,其中AE= AB,BF=
AB,BF= BC,CG=
BC,CG= CD,DH=
CD,DH= DA,连结E、F、G、H.求四边形EFGH的面积是四边形ABCD的面积的________(如图).
DA,连结E、F、G、H.求四边形EFGH的面积是四边形ABCD的面积的________(如图).

分析:如下图:连结ED和BD,因为DH=
 DA,所以S△AEH=
DA,所以S△AEH= S△AED,因为AE=
S△AED,因为AE= AB,S△AED=
AB,S△AED= S△ABD,所以S△AEH=
S△ABD,所以S△AEH= ×
× S△ABD=
S△ABD= S△ABD,CG=
S△ABD,CG= CD,DH=
CD,DH= DA,S△CGF=
DA,S△CGF= S△BCD,因此S△AEH+S△CGF=
S△BCD,因此S△AEH+S△CGF= (S△ABD+S△BCD)=
(S△ABD+S△BCD)= S□ABCD,同理S△BFE+S△DHG=
S□ABCD,同理S△BFE+S△DHG= S□ABCD,所以S△AEH+S△CGF+S△BFE+S△DHG=
S□ABCD,所以S△AEH+S△CGF+S△BFE+S△DHG= S□ABCD,
S□ABCD,解答:
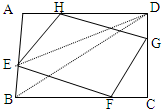 解:连结ED和BD,因为DH=
解:连结ED和BD,因为DH= DA,所以S△AEH=
DA,所以S△AEH= S△AED
S△AED因为AE=
 AB,所以S△AED=
AB,所以S△AED= S△ABD,
S△ABD,所以S△AEH=
 ×
× S△ABD=
S△ABD= S△ABD,
S△ABD,同理CG=
 CD,DH=
CD,DH= DA,所以S△CGF=
DA,所以S△CGF= S△BCD,
S△BCD,因此S△AEH+S△CGF=
 (S△ABD+S△BCD)=
(S△ABD+S△BCD)= S□ABCD,
S□ABCD,同理S△BFE+S△DHG=
 S□ABCD,
S□ABCD,所以S△AEH+S△CGF+S△BFE+S△DHG=
 S□ABCD,
S□ABCD,所以S□EFGH=(1-
 )S□ABCD=
)S□ABCD= S□ABCD.
S□ABCD.即四边形EFGH的面积是四边形ABCD面积的
 .
.答:四边形EFGH的面积是四边形ABCD的面积的
 .
.故答案为:
 .
.点评:本题主要是利用高一定时,面积的比等于对应底的比解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
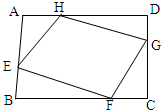 ABCD为任意四边形,其中AE=
ABCD为任意四边形,其中AE=