题目内容
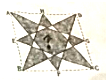
5.如图,在一个梯形内有两个三角形的面积分别为12和16,已知上底是下底的$\frac{3}{4}$,求阴影部分的面积?
分析 根据梯形的上底是下底的$\frac{3}{4}$,可看作上底是3a,下底是4a,计算出两个空白三角形的高,两高之和即梯形的高,然后计算出梯形的面积,最后即可求出阴影部分的面积.据此解答.
解答 解:已知梯形的上底是下底的$\frac{3}{4}$,那么上底和下底可分别看作是3a和4a.
三角形的高分别为:
12×2÷3a=$\frac{8}{a}$
16×2÷4a=$\frac{8}{a}$
梯形的面积为:
(3a+4a)×($\frac{8}{a}$+$\frac{8}{a}$)÷2
=7a×$\frac{16}{a}$÷2
=56
阴影部分的面积为:
56-(12+16)=28
答:阴影部分的面积是28.
点评 此题主要考查三角形面积公式及梯形面积公式的应用.

练习册系列答案
相关题目
15.用竖式计算.
| 32×18= | 35×24= | 12×96= |
| 34×25= | 29×41= | 86×17= |
12.下列数中,是合数的有( )
| A. | 7 | B. | 23 | C. | 91 | D. | 19 |