题目内容
 摸牌游戏.
摸牌游戏.从一副扑克牌中抽出某种花色的牌13张,将这些牌反扣在桌面上.甲、乙二人做下面的游戏:
(1)每次摸两张,然后放回去,另一个人再摸.
(2)两张牌的点数之和是双数时甲加1分,是单数时乙加1分.
(3)分数高者为胜.
分析:每次摸两张,然后放回去,另一个人再摸;共有1、3、5、7、9、11、13,七张单数牌;2、4、6、8、10、12,六张双数牌,从13张卡片中,任何抽两张,根据:单数+单数=偶数,单数+偶数=单数,偶数+偶数=偶数,可知:和是单数的可能性大,和是双数的可能性小,所以不公平;可以改为:每次摸一张,然后放回去,另一个人再摸,大于7的甲加1分,小于7的乙加1分;据此判断.
解答:解:因为共有1、3、5、7、9、11、13,七张单数牌;2、4、6、8、10、12,六张双数牌,从13张卡片中,任何抽两张,根据:单数+单数=偶数,单数+偶数=单数,偶数+偶数=偶数,可知:和是单数的可能性大,和是双数的可能性小,所以不公平;
可以改为:每次摸一张,然后放回去,另一个人再摸,大于7的甲加1分,小于7的乙加1分,这样公平.
可以改为:每次摸一张,然后放回去,另一个人再摸,大于7的甲加1分,小于7的乙加1分,这样公平.
点评:本题考查的是游戏公平性的判断,注意概率相等就公平,否则就不公平.

练习册系列答案
相关题目
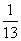 ,他说得对吗?
,他说得对吗?