题目内容
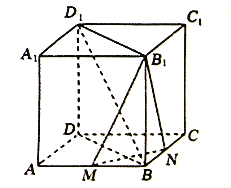
【题目】若图，在正方体
中， 
分别是
的中点.
（1）求证：平面
平面
；
（2）在棱
上是存在一点
，使得
平面
，若存在，求
的值；若不存在，说明理由.
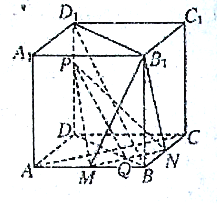
【答案】（1）证明过程见解析；(2) 
【解析】试题分析：（1）连接
，由正方形性质得
，又由正方体
中， 
， 
分别是
， 
的中点，易得
，则
， 
，由线面垂直的判定定理，可得
平面
，进而由面面垂直的判定定理，可得平面
平面
；（2）设
与
的交点是
，连接
， 
， 
，由线面平行的性质定理，我们易由
平面
， 
平面
，平面
平面
，得
，再由平行线分线段成比例定理，得到线段
与
的比.
试题解析：（1）证明：连接
，则
，又
分别是
的中点，
所以
，所以
，因为
是正方体，
所以
平面
，因为
平面
，所以
，
因为
，所以
平面
。
(2)设
与
的交点是
，连接
，
因为
平面
平面
，平面
平面
，
所以
练习册系列答案
相关题目
【题目】下面是二（1）班同学最喜欢哪个季节的调查情况。
春季：正正正正正 夏季：○○○○○○○○○○○
秋季：√√√√√√√√ 冬季：
（1）请你根据上面记录的结果，完成下表。
季节 | 春 | 夏 | 秋 | 冬 |
人数（人） | ________ | ________ | ________ | ________ |
（2）二（1)班喜欢________季的人数最多。
（3）喜欢________季的人数比喜欢________季的人数多________人。
（4）如果组织二（1)班同学去游玩，最好应安排在________季，因为________．