题目内容
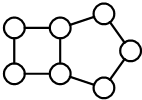 将1、2、…7这7个数字填入图中的七个小圆内,使左侧的四个小圆内的数字之和是15,右侧的5个小圆内的数字之和是25,则有
将1、2、…7这7个数字填入图中的七个小圆内,使左侧的四个小圆内的数字之和是15,右侧的5个小圆内的数字之和是25,则有24
24
种不同的填法.分析:根据题意,设左侧的四个小圆与右侧的5个小圆内共用的两个小圆的数是A和B,那么它们的和是:1+2+3+4+5+6+7+A+B=15+25,求出A和B,然后再进一步解答即可.
解答:解:设共用的两个小圆的数是A和B;
根据题意可得:
1+2+3+4+5+6+7+A+B=15+25,
A+B=12;
1到7中,只有5+7=12,所以,共用的两个数分别是5和7;这时有2种不同填法;
左侧的四个圆中,剩下的两个圆的和是:15-12=3;只有1+2=3;所以剩下的填1和2;这时也有2种不同填法;
还剩下3,4,6,填在右侧的3个圆中,这时有6种不同填法;
由乘法原理可得:共有2×2×6=24(种).
答:有24种不同的填法.
故答案为:24.
根据题意可得:
1+2+3+4+5+6+7+A+B=15+25,
A+B=12;
1到7中,只有5+7=12,所以,共用的两个数分别是5和7;这时有2种不同填法;
左侧的四个圆中,剩下的两个圆的和是:15-12=3;只有1+2=3;所以剩下的填1和2;这时也有2种不同填法;
还剩下3,4,6,填在右侧的3个圆中,这时有6种不同填法;
由乘法原理可得:共有2×2×6=24(种).
答:有24种不同的填法.
故答案为:24.
点评:本题的关键是求出共用的两个小圆的数,然后再根据题意进一步解答即可.

练习册系列答案
相关题目
 右图是一个奥林匹克五环标识.这五个环相交成9部分A、B、C、D、E、F、G、H、I.请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中,使得五个环内的数字和恰好构成五个连续的自然数.问:这五个连续自然数的和的最大值是多少?
右图是一个奥林匹克五环标识.这五个环相交成9部分A、B、C、D、E、F、G、H、I.请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中,使得五个环内的数字和恰好构成五个连续的自然数.问:这五个连续自然数的和的最大值是多少?