题目内容
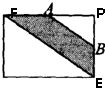
 如图,已知长方形面积是56平方厘米,A、B分别是长和宽的中点,则阴影部分的面积是
如图,已知长方形面积是56平方厘米,A、B分别是长和宽的中点,则阴影部分的面积是21
21
平方厘米.分析:(1)根据长方形的对角线的性质可得,一条对角线把长方形分成了面积相等的两个三角形,由此可以求得三角形PEF的面积为56÷2=28平方厘米;
(2)A、B分别是长和宽的中点,所以三角形PAB与三角形PEF相似,相似比是1:2,则它们的面积之比是1:4,由此即可得出阴影部分的面积是三角形PEF面积的
.
(2)A、B分别是长和宽的中点,所以三角形PAB与三角形PEF相似,相似比是1:2,则它们的面积之比是1:4,由此即可得出阴影部分的面积是三角形PEF面积的
| 3 |
| 4 |

解答:解:A、B分别是长和宽的中点,所以三角形PAB与三角形PEF相似,相似比是1:2,则它们的面积之比是1:4,
所以阴影部分的面积是三角形PEF面积的1-
=
,
所以阴影部分的面积是:56÷2×
=21(平方厘米);
答:阴影部分的面积是21平方厘米.
故答案为:21.
所以阴影部分的面积是三角形PEF面积的1-
| 1 |
| 4 |
| 3 |
| 4 |
所以阴影部分的面积是:56÷2×
| 3 |
| 4 |
答:阴影部分的面积是21平方厘米.
故答案为:21.
点评:此题考查了相似三角形的性质以及长方形的对角线把长方形分成两个面积相等的三角形的性质的灵活应用.

练习册系列答案
相关题目

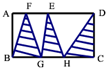 如图,已知长方形的长为20厘米,宽10厘米,求图中阴影部分的面积.
如图,已知长方形的长为20厘米,宽10厘米,求图中阴影部分的面积.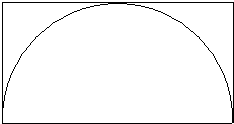 (2010?茶陵县模拟)如图,已知长方形的面积为12平方厘米,求半圆面积.
(2010?茶陵县模拟)如图,已知长方形的面积为12平方厘米,求半圆面积. 如图,已知长方形面积是56平方厘米,A、B分别是长和宽的中点,则阴影部分的面积是________平方厘米.
如图,已知长方形面积是56平方厘米,A、B分别是长和宽的中点,则阴影部分的面积是________平方厘米.