题目内容
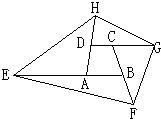 如图,ABCD是一个四边形,它的面积是1,延长BA到E,使AE=2BA;延长AD到H,使DH=AD;延长DC到G,使CG=2DC;延长CB到F,使BF=CB.那么四边形EFGH的面积是
如图,ABCD是一个四边形,它的面积是1,延长BA到E,使AE=2BA;延长AD到H,使DH=AD;延长DC到G,使CG=2DC;延长CB到F,使BF=CB.那么四边形EFGH的面积是8
8
.分析:根据四边形ABCD的面积是1,要求四边形EFGH的面积,只要求出四边形ABCD四周多出来的四个三角形的面积之和即可解决问题.
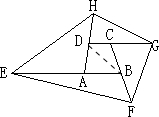

解答:解:连接AC,
对△AEH分析,可知其底AE=2AB,其高即H到AB的距离为H到AE距离的2倍,
所以△AEH的底是△ABD底的2倍,前者高为后者的2倍,
于是△AEH的面积为△ABD的面积的2×2=4倍,
同理,△BEF的面积为△BCD面积的3倍,
△FCG是△BCD的面积的4倍,
△HDG是△ABD的面积的3倍,
所以多出来的这四个三角形的面积之和是:4△ABD+3△BCD+4△BCD+3△ABD=7(△ABD+△BCD)=7×1=7,
所以三角形EFGH的面积是:7+1=8.
答:四边形EFGH的面积是8.
故答案为:8.
对△AEH分析,可知其底AE=2AB,其高即H到AB的距离为H到AE距离的2倍,
所以△AEH的底是△ABD底的2倍,前者高为后者的2倍,
于是△AEH的面积为△ABD的面积的2×2=4倍,
同理,△BEF的面积为△BCD面积的3倍,
△FCG是△BCD的面积的4倍,
△HDG是△ABD的面积的3倍,
所以多出来的这四个三角形的面积之和是:4△ABD+3△BCD+4△BCD+3△ABD=7(△ABD+△BCD)=7×1=7,
所以三角形EFGH的面积是:7+1=8.
答:四边形EFGH的面积是8.
故答案为:8.
点评:解答此题的关键是,根据题意,添加辅助线,利用三角形的面积公式,帮助我们找到三角形之间的关系,由此即可解答.

练习册系列答案
相关题目
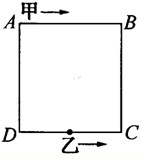 如图,ABCD是一个边长为6米的模拟跑道,甲玩具车从A出发顺时针行进,速度是每秒5厘米,乙玩具车从CD的中点出发逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走多少厘米?
如图,ABCD是一个边长为6米的模拟跑道,甲玩具车从A出发顺时针行进,速度是每秒5厘米,乙玩具车从CD的中点出发逆时针行进,结果两车第二次相遇恰好是在B点,求乙车每秒走多少厘米? (2012?长清区模拟)(如图)ABCD是一个长方形.三角形ADE比三角形CEF的面积小10平方米.问CF的长是多少厘米?
(2012?长清区模拟)(如图)ABCD是一个长方形.三角形ADE比三角形CEF的面积小10平方米.问CF的长是多少厘米?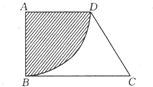 如图,ABCD是一个直角梯形,已知AD:BC=3:5,且阴影部分面积是6.28cm2,问梯形ABCD的面积是多少cm2?
如图,ABCD是一个直角梯形,已知AD:BC=3:5,且阴影部分面积是6.28cm2,问梯形ABCD的面积是多少cm2?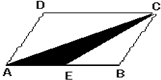 如图,ABCD是一个平行四边形,它的面积是96M2,E是AB的中点,那么阴影部分的面积是
如图,ABCD是一个平行四边形,它的面积是96M2,E是AB的中点,那么阴影部分的面积是