题目内容
 (2012?合肥)如图是一个长5厘米、宽3厘米的长方形.
(2012?合肥)如图是一个长5厘米、宽3厘米的长方形.(1)在长方形中画一条线段,把它分成一个最大的等腰直角三角形和一个梯形.
(2)求直角三角形的面积.
(3)以等腰直角三角形的一个直角边所在的直线为轴,将三角形旋转,可以形成一个
圆锥体
圆锥体
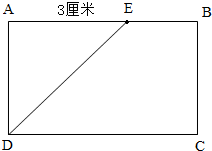
.算出旋转形成的这个图形的体积.(得数保留两位小数)分析:(1)把它分成一个最大的等腰直角三角形,那么这个直角三角形的直角边的长度就是这个长方形宽的长度;先以长方形的顶点A为端点,在长上截去一条3厘米的线段,然后连接这条线段另一个端点E和长方形的顶点D,这样就把长方形分成了一个等腰直角三角形AED,和一个直角梯形BCDE;
(2)直角三角形的直角边长度都是3厘米,根据三角形的面积公式求解即可;
(3)如果以这个等腰直角形的直角边为轴,旋转后所组成的图形是一个底面半径为3厘米,高为3厘米的圆锥.根据圆锥的体积公式V=
πr2h即可求出圆锥的体积
(2)直角三角形的直角边长度都是3厘米,根据三角形的面积公式求解即可;
(3)如果以这个等腰直角形的直角边为轴,旋转后所组成的图形是一个底面半径为3厘米,高为3厘米的圆锥.根据圆锥的体积公式V=
| 1 |
| 3 |
解答:解:(1)下图中的三角形AED就是要求的三角形,梯形BCDE就是要求的梯形;
(2)3×3÷2=4.5(平方厘米);
答:直角三角形的面积4.5平方厘米.
(3)以等腰直角三角形的一个直角边所在的直线为轴,将三角形旋转,可以形成一个底面半径为3厘米,高为3厘米的圆锥;
体积是:
3.14×32×3×
,
=3.14×9×3×
,
=28.26(立方厘米),
答:以直角边为轴旋转一周所形成图形是圆锥体,它的体积是28.26立方厘米.
故答案为:圆锥体.

(2)3×3÷2=4.5(平方厘米);
答:直角三角形的面积4.5平方厘米.
(3)以等腰直角三角形的一个直角边所在的直线为轴,将三角形旋转,可以形成一个底面半径为3厘米,高为3厘米的圆锥;
体积是:
3.14×32×3×
| 1 |
| 3 |
=3.14×9×3×
| 1 |
| 3 |
=28.26(立方厘米),
答:以直角边为轴旋转一周所形成图形是圆锥体,它的体积是28.26立方厘米.
故答案为:圆锥体.
点评:本题分割图形关键是知道等腰直角三角形腰的长度;还考查了一个简单图形绕一轴旋转一周所组成的图形是什么图形,以及圆锥的体积计算.

练习册系列答案
相关题目
 (2012?合肥)如图是甲、乙、丙三人独做一项工程所需天数的统计图,请看图解决下列问题.
(2012?合肥)如图是甲、乙、丙三人独做一项工程所需天数的统计图,请看图解决下列问题.