题目内容
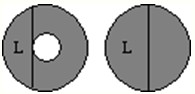 图中左图是一个圆环上是圆环内最长的线段,右图是以L为直径的圆.则左图中的圆环和右图中的圆的面积比是
图中左图是一个圆环上是圆环内最长的线段,右图是以L为直径的圆.则左图中的圆环和右图中的圆的面积比是1:1
1:1
.分析:如图,L为圆环中小圆的切线,分别画出左边圆环的小圆半径r和大圆半径R,则OP⊥L,根据勾股定理和圆与圆环的面积公式即可进行推理解答.
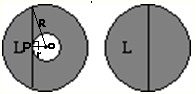

解答:解:根据勾股定理可得:R2-r2=(
)2;
而根据圆环的面积公式可得:圆环的面积=π(R2-r2);
所以圆环的面积=π(
)2;
圆的面积=π(
)2;
所以圆环的面积与圆的面积之比是:π(
)2:π(
)2=1:1.
故答案为:1:1.
| L |
| 2 |
而根据圆环的面积公式可得:圆环的面积=π(R2-r2);
所以圆环的面积=π(
| L |
| 2 |
圆的面积=π(
| L |
| 2 |
所以圆环的面积与圆的面积之比是:π(
| L |
| 2 |
| L |
| 2 |
故答案为:1:1.
点评:此题主要考查学生对切线的性质及勾股定理的理解运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目