题目内容
 列式解答.
列式解答.
①明新手机厂原计划每天生产手机80部,25天完成任务.实际每天多生产手机20部,实际用几天完成任务?
②李敏和他爸爸今年的年龄一共是54岁,爸爸的年龄是李敏的3.5倍,李敏今年多少岁?(用方程解)
③有一天,吴叔叔和李伯伯两人乘同一辆出租车回家,付了36元车费.吴叔叔到家的路程刚好是李伯伯到家路程的一半,如果按乘车路程付钱,他俩各应付车费多少元?
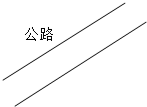
④李村计划从村里修一条水泥路连到公路上(见图).请你根据下面的要求,帮助李村求出修路的实际距离.
要求:①画:画出修路的最近路线(画在图中);②量:量出李村到公路的图上距离;③算:李村到公路的实际距离是多少米?
李村?
量出图上距离是:________
比例尺1:40000 算出实际距离是:
⑤红星小学一间会议室的地面是长9米,宽6米的长方形.市场上出售两种质量相同的瓷方砖:面积0.25平方米的瓷方砖每块10元,面积0.36平方米的瓷方砖每块18元.如果要买其中一种瓷方砖铺满这间会议室,请你帮校长算一算,买哪一种砖更省钱?
2厘米
分析:①先求出总生产量,再求出实际的效率,然后用总生产量除以实际的效率就是实际需要的时间;
②设李敏的年龄是x岁,爸爸的年龄就是3.5x岁,然后根据李敏和他爸爸今年的年龄一共是54岁列出方程;
③吴叔叔到家的路程刚好是李伯伯到家路程的一半,那么吴叔叔应付的钱数与李伯伯应付钱数比是1:2,把36元按照这个比例分配即可;
④最近路线就是李村到公路的垂线段,画出这个垂线段;然后量出这个垂线段的长度;再用这个长度除以比例尺求出实际的距离;
⑤先求出会议室的面积,然后分别求出两种瓷砖的面积求出各需要多少块,进而求出需要的钱数,再比较选择.
解答:①(80×25)÷(80+20),
=2000÷100,
=20(天);
答:实际用20天完成任务.
②设李敏的年龄是x岁,由题意得:
3.5x+x=54,
4.5x=54,
x=12;
答:李敏的年龄是12岁.
③吴叔叔应付的钱数与李伯伯应付钱数比是1:2,
1+2=3;
36× =12(元);
=12(元);
36-12=24(元);
答:吴叔叔应付12元,李伯伯应付24元.
④图如下:

量的图上距离是2厘米;
2÷ =80000(厘米);
=80000(厘米);
80000厘米=800(米);
答:图上距离是2厘米,实际距离是800米.
⑤9×6=54(平方米);
54÷0.25×10,
=216×10,
=2160(元);
54÷0.36×18,
=150×18,
=2700(元);
2160<2700;
答:买面积是0.25平方米的砖更省钱.
点评:本题关键是分清数量关系,把实际问题转化成数学问题,再根据数学的数量关系求解.
分析:①先求出总生产量,再求出实际的效率,然后用总生产量除以实际的效率就是实际需要的时间;
②设李敏的年龄是x岁,爸爸的年龄就是3.5x岁,然后根据李敏和他爸爸今年的年龄一共是54岁列出方程;
③吴叔叔到家的路程刚好是李伯伯到家路程的一半,那么吴叔叔应付的钱数与李伯伯应付钱数比是1:2,把36元按照这个比例分配即可;
④最近路线就是李村到公路的垂线段,画出这个垂线段;然后量出这个垂线段的长度;再用这个长度除以比例尺求出实际的距离;
⑤先求出会议室的面积,然后分别求出两种瓷砖的面积求出各需要多少块,进而求出需要的钱数,再比较选择.
解答:①(80×25)÷(80+20),
=2000÷100,
=20(天);
答:实际用20天完成任务.
②设李敏的年龄是x岁,由题意得:
3.5x+x=54,
4.5x=54,
x=12;
答:李敏的年龄是12岁.
③吴叔叔应付的钱数与李伯伯应付钱数比是1:2,
1+2=3;
36×
 =12(元);
=12(元);36-12=24(元);
答:吴叔叔应付12元,李伯伯应付24元.
④图如下:

量的图上距离是2厘米;
2÷
 =80000(厘米);
=80000(厘米);80000厘米=800(米);
答:图上距离是2厘米,实际距离是800米.
⑤9×6=54(平方米);
54÷0.25×10,
=216×10,
=2160(元);
54÷0.36×18,
=150×18,
=2700(元);
2160<2700;
答:买面积是0.25平方米的砖更省钱.
点评:本题关键是分清数量关系,把实际问题转化成数学问题,再根据数学的数量关系求解.

练习册系列答案
相关题目
 (2004?南安市)列式解答.
(2004?南安市)列式解答.