Question

一个由棱长为l厘米的小正方体组合成的大正方体（如右图），数一数，其中大、小正方体一共有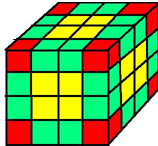

100

个．

Answer 1

分析：要求一共有大、小正方体多少个，可以分类考虑，即棱长分别是1厘米、2厘米、3厘米、4厘米的，然后分别数出即可，注意棱长是2厘米的正方体，要从顶角、棱的中间、面的中心、大正方体的中心并结合正方体的特征去计算．

解答：解：（1）棱长是1厘米的正方体有：4×4×4=64（个）；
（2）棱长是2厘米的正方体分四种情况考虑：
①在每个顶角上有一个，因为正方体有8个顶角，所以共有：1×8=8（个）；
②在每条棱的中间有一个，因为正方体有12条棱，所以共有：1×12=12（个）；
③在每个面的中心有一个，因为正方体有6个面，所以共有：1×6=6（个）；
④在大正方体的中心，还有1个没有露出面的；
（3）棱长是3厘米的正方体只在8个顶角上，所以有：1×8=8（个）；
（4）棱长是4厘米的正方体即是这1个最大的正方体；
所以，大、小正方体一共有：
64+8+12+6+1+8+1=100（个）；
答：其中大、小正方体一共有 100个．
故答案为：100．

点评：本题能找到分类从顶角、棱的中间、面的中心、大正方体的中心去数正方体的个数的方法是关键．