题目内容
【题目】已知函数![]() (
(![]() 且
且![]() )是定义在
)是定义在![]() 上的奇函数.
上的奇函数.
(1)求实数![]() 的值;
的值;
(2)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) a=2 (2) m≤0
【解析】试题分析:
(1)可先由奇函数的必要条件![]() (
(![]() 存在时)求得
存在时)求得![]() 值,然后检验满足
值,然后检验满足![]() 即可;
即可;
(2)在![]() 时,不等式
时,不等式![]() 可变为
可变为![]() 恒成立,因此只要求得
恒成立,因此只要求得![]() 在
在![]() 时的最小值即可得出
时的最小值即可得出![]() 的范围,为此可用换元法,设
的范围,为此可用换元法,设![]() ,再利用函数的单调性求得最小值.
,再利用函数的单调性求得最小值.
试题解析:
(1):∵f(x)是定义在R上的奇函数.
∴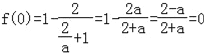 ,
,
∴a=2.
∴![]() ,
,
∴![]() ,
,
∴f(x)是定义在R上的奇函数.
∴a=2.
(2)由题意得,当x≥1时,![]()
即![]() 恒成立,
恒成立,
∵x≥1,
∴2x≥2,
∴![]() 恒成立,
恒成立,
设t=2x﹣1(t≥1),
则![]()
设![]() ,
,
则函数g(t)在t∈[1,+∞)上是增函数.
∴g(t)min=g(1)=0,
∴m≤0,
∴实数m的取值范围为m≤0.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
【题目】几个城市之间的路程如下表:(单位:千米)
北京——沈阳 | 北京——济南 | 北京——石家庄 | 济南——青岛 |
687 | 409 | 300 | 351 |
(1)从北京到济南再到青岛的路程是多少千米?
(2)从北京到沈阳比从北京到石家庄远多少千米?