题目内容
4.公司里有三台机器出现了不同程度的故障,已知第一台修复时间需要8分钟,第二台修复时间需要30分钟,第三台需要修复时间15分钟,每台机器停产1分钟造成经济损失500元,现只有一名修理工,那么怎样安排才能使修复时间最短,且经济损失最少?分析 台车床同时出现故障,需要修理,有1台车床修理时,其他两台机床就要等着,由此可以看出自然是先修理花时间少的车床,这样才能使它们等候时间的总和最少,每台车床停产1分钟的经济损失为500元,用最少的等候时间总和再乘500,就是最少的经济损失.
解答 解:先修理第一台,再修理第三台,最后修理第二台,等候时间总和是:
8×3+15×2+30,
=24+30+30,
=84(分钟),
所以最少的经济损失是:84×500=42000(元)
答:先修理第一台,再修理第三台,最后修理第二台,最少的经济损失是42000元.
点评 解答这类题目的关键是要优化组合,找到优化组合的突破点,在这里是按时间少的先修理进行排序即可.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
14.口算
| 150×6= | 725-65= | 350×2= | 230×4= |
| 140÷20= | 2700÷300= | 560÷40= | 102+20= |
12.一列火车可乘人数如表:
这列火车可乘多少人?
| 车厢种类 | 车厢节数 | 每节车厢可乘人数 |
| 硬座 | 7 | 108 |
| 硬卧 | 16 | 78 |
| 软卧 | 4 | 34 |
19.直接写得数.
| $\frac{2}{5}$+$\frac{3}{5}$= | $\frac{3}{4}$-$\frac{3}{8}$= | 1-$\frac{1}{6}$= | 1-$\frac{4}{7}$-$\frac{3}{7}$= |
| $\frac{1}{8}$-0.125= | $\frac{1}{3}$+$\frac{3}{11}$= | 10+$\frac{8}{9}$= | $\frac{5}{13}$+$\frac{8}{13}$-$\frac{8}{13}$+$\frac{5}{13}$= |
14.C是平行四边形底边的中点,甲乙两个三角形面积有什么关系?( )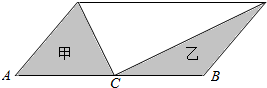

| A. | 甲三角形面积大 | B. | 乙三角形面积大 | ||
| C. | 两个三角形面积相等 |