Question

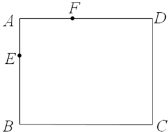如图是一个长为15cm、宽为12cm的长方形，AE=4cm，AF=6cm．在长方形的边界上再选一点，使得这一点与E、F两点连成的三角形的面积尽可能大．这个三角形的最大面积是

 

cm²．

Answer 1

考点：三角形的周长和面积

专题：平面图形的认识与计算

分析：因为三角形的面积=底×高÷2，所以三角形EFP的面积=

1

2

×EF×h，h是P点到EF的距离，所以要使三角形EFP的面积尽可能大，那么h应尽可能大，C点到EF的距离最远，所以，P点应该选在C点，此时面积才最大．
三角形EFP的面积=正方形面积-三角形AEF面积-三角形BFC面积-三角形DEC面积，代入数值计算即可解答．

解答： 解：如图

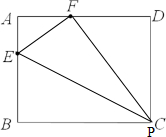
三角形EFP的面积=长方形面积-三角形AEF面积-三角形BEC面积-三角形DFC面积
=15×12-6×4÷2-（15-6）×12÷2-（12-4）×15÷2
=180-12-54-60，
=54cm²；
答：最大的可能是54cm²．
故答案为：54．

点评：解答本题的关键是找出符合条件的P点，然后根据面积公式计算．