题目内容
小王和小李各有一张相同的长方形铁片,长100厘米,宽80厘米.老师要他们在四角各剪去一个相等面积的正方形,做成一个无盖的长方体盒子,小王的设计如甲图,小李设计如乙图.谁设计的盒子的容积大?若让你设计,你怎么才能使盒子的容积更大?
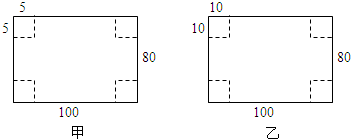

分析:根据题意可知:在长100厘米,宽80厘米长方形铁片的四角各剪去一个相等面积的正方形,做成一个无盖的长方体盒子,要使盒子的容积最大,也就是长、宽、高相差越小,容积就越大.据此解答.
解答:解:小王的设计:
(100-5×2)×(80-5×2)×5,
=90×70×5,
=31500(立方厘米);
小李的设计:
(100-10×2)×(80-10×2)×10,
=80×60×10,
=48000(立方厘米);
答:小李设计的容积大一些,是48000立方厘米.
我的设计:
(100-15×2)×(80-15×2)×15,
=70×50×15,
=52500(立方厘米);
答:剪出边长是15厘米的正方形后做成的盒子容积最大,是52500立方厘米.
(100-5×2)×(80-5×2)×5,
=90×70×5,
=31500(立方厘米);
小李的设计:
(100-10×2)×(80-10×2)×10,
=80×60×10,
=48000(立方厘米);
答:小李设计的容积大一些,是48000立方厘米.
我的设计:
(100-15×2)×(80-15×2)×15,
=70×50×15,
=52500(立方厘米);
答:剪出边长是15厘米的正方形后做成的盒子容积最大,是52500立方厘米.
点评:此题解答关键是明确:做成盒子的长、宽、高相差越小,容积就越大.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目