题目内容
11．用一根铁丝围成正方形、长方形、正三角形和半圆，那么面积最大的是（ ）| A． | 长方形 | B． | 正方形 | C． | 正三角形 | D． | 半圆 |
分析 根据题意和四个选项的几何图形的面积公式，假设这根绳子的长是6.28分米，分别求出面积后进行比较选择即可．
解答 解：根据三角形面积推导公式可知，周长相等的情况下，三角形面积一定小于正方形和长方形；
由此再比较半圆、正方形及长方形在周长相等的情况下，哪种图形面积最大；
设这根绳子的长是6.28分米，
则正方形的面积是：（6.28÷4）2=2.4649（平方分米）；
长方形一条长和宽的和是6.28÷2=3.14（分米），设这个长方形的长、宽分别为a、b：
取一些数字（0.1，3.04），（0.5，2.64），（1，2.14）…，
可以发现长方形的长和宽越接近，面积就越大，当长和宽相等时，也就是变成正方形了，
所以这个长方形的面积一定小于正方形的面积．
半圆的面积是：半圆的半径是r，则2r+3.14×r=6.28，所以r≈1.2
3.14×1.22÷2=3.14×1.44÷2=2.268（平方分米）；
所以正方形的面积最大．
故选：B．
点评 考查了周长相同的图形在所有图形中，圆的面积最大，但此题围成的是半圆．
练习册系列答案
全能测控一本好卷系列答案
相关题目
2．下面的图象表示在同一地点、同一时间，测得的不同物体的高度和它的影长之间的关系．
（1）看图填写下表．
（2）根据图象推算，如果一个物体的高度是6.5米，这时它的影长是3.9米．
（3）物体的高度和它的影长成正比例．
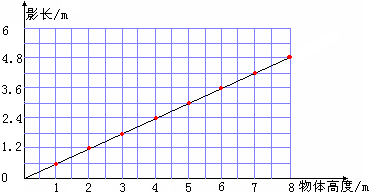
（1）看图填写下表．
| 物体高度/m | 1 | 2 | 3 | 4 | … |
| 影 长/m | … |
（3）物体的高度和它的影长成正比例．
19．
小强去游乐园玩．
（1）如果只玩碰碰车，能玩几次，还剩多少钱？
（2）我带了20元钱，来回坐公交车用了2元，其余的全部玩了游戏．我玩了什么
游戏呢？
方案一：他可以玩2次射击
方案二：他可以玩3次卡丁车．
小强去游乐园玩．| 游戏名称 | 碰碰车 | 过山车 | 蹦蹦床 | 卡丁车 | 射击 |
| 价格（元/每人每次） | 8元 | 7元 | 5元 | 6元 | 9元 |
（2）我带了20元钱，来回坐公交车用了2元，其余的全部玩了游戏．我玩了什么
游戏呢？
方案一：他可以玩2次射击
方案二：他可以玩3次卡丁车．
20．直接写出计算结果．
| 2.5×4= | 1-$\frac{3}{7}$= | $\frac{1}{2}$+$\frac{1}{3}$= | 1.6-0.56= |
| 1.7+0.4= | $\frac{4}{7}$+$\frac{5}{7}$= | 2-$\frac{2}{3}$= | $\frac{1}{5}$+$\frac{1}{3}$+$\frac{4}{5}$= |
1．整存整取定期储蓄存单．
根据上面的存单，列式求出这笔存款到期时，储蓄所应付出本金和利息共多少元．
| 存入日 | 存期 | 到期日 | 年利率 | ||
| 2001年6月23日 | 3年 | 2004年6月23日 | 2.7% | ||
| 帐号 3128643 户名：叶山武 存入人民币 叁万元整￥30000 天一路储蓄所（盖章） | |||||
| 支取日 | 实付本金 | 利息 | 本息合计 | ||