题目内容

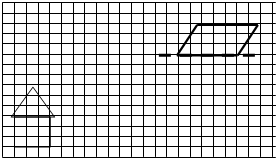
(1)画出图1的另一半,使它成为一个轴对称图形.
(2)把图2绕A点顺时针旋转90°.并算出这个组合图形的周长和面积.
(3)画一个与图3面积相等的三角形,再把这个三角形按2:1放大.
(4)把图4向右平移4格.
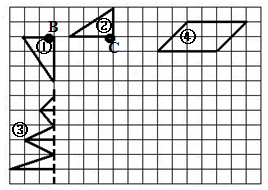
解:根据分析作图如下:

(2)组合图形的周长为:3.14×2+2×2
=6.28+4,
=10.28;
组合图形的面积为:3.14×12=3.14;
(3)平行四边形的面积为:2×3=6,
三角形的面积为:底×高÷2=6,即底×高=12,
那么三角形的底与高可分别为:3与4,
按照2:1放大后的底与高可分别为:6与8.
分析:(1)根据作轴对称图形的方法,先找到图1的对称轴,然后再进行作图即可;
(2)旋转90度后的组合图形是两个同样大的半圆,半圆的直径为2,半径则为1,那么这个组合图形的周长等于半圆所在圆的周长再加两条直径的长;组合图形的面积就是半圆所在圆的面积,列式解答即可;
(3)根据平行四边形的面积公式底×高确定平行四边形的面积即三角形的面积,然后再根据三角形的面积公式底×高÷2确定三角形的底与高,作图即可;最后将三角形的底与高分别按2:1放大后再次作图即可;
(4)将图形4向右平移4个格后再作图即可.
点评:解答此题的关键是:(1)找准对称轴,然后再作图;
(2)利用圆的周长公式和圆的面积公式进行解答即可;
(3)利用平行四边形的面积公式和三角形的面积公式确定三角形的高与底分别是多少,然后再作图即可;
(4)直接平移后作图即可.

(2)组合图形的周长为:3.14×2+2×2
=6.28+4,
=10.28;
组合图形的面积为:3.14×12=3.14;
(3)平行四边形的面积为:2×3=6,
三角形的面积为:底×高÷2=6,即底×高=12,
那么三角形的底与高可分别为:3与4,
按照2:1放大后的底与高可分别为:6与8.
分析:(1)根据作轴对称图形的方法,先找到图1的对称轴,然后再进行作图即可;
(2)旋转90度后的组合图形是两个同样大的半圆,半圆的直径为2,半径则为1,那么这个组合图形的周长等于半圆所在圆的周长再加两条直径的长;组合图形的面积就是半圆所在圆的面积,列式解答即可;
(3)根据平行四边形的面积公式底×高确定平行四边形的面积即三角形的面积,然后再根据三角形的面积公式底×高÷2确定三角形的底与高,作图即可;最后将三角形的底与高分别按2:1放大后再次作图即可;
(4)将图形4向右平移4个格后再作图即可.
点评:解答此题的关键是:(1)找准对称轴,然后再作图;
(2)利用圆的周长公式和圆的面积公式进行解答即可;
(3)利用平行四边形的面积公式和三角形的面积公式确定三角形的高与底分别是多少,然后再作图即可;
(4)直接平移后作图即可.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 (1)画出小房图向右平移6格后的图形.
(1)画出小房图向右平移6格后的图形.


 按要求画一画,填一填.
按要求画一画,填一填.