题目内容
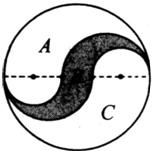 如图,大圆直径上的黑点是五等分点,则A、B、C三部分的面积比为
如图,大圆直径上的黑点是五等分点,则A、B、C三部分的面积比为2:1:2
2:1:2
.分析:可把三个圆分别定义为小圆、中圆、大圆,设小圆的半径是r,则根据大圆直径上的黑点是五等分点,可知中圆的半径为
r,大圆的半径为
r,
可以先分别求出三个圆一半的面积,然后用中圆面积的一半减去小圆面积的一半就是阴影部分面积的一半,用大圆面积的一半减去中圆面积的一半就是C部分除掉小圆面积一半后的面积,最后把所求出的三部分的面积进行相比即可.
| 3 |
| 2 |
| 5 |
| 2 |
可以先分别求出三个圆一半的面积,然后用中圆面积的一半减去小圆面积的一半就是阴影部分面积的一半,用大圆面积的一半减去中圆面积的一半就是C部分除掉小圆面积一半后的面积,最后把所求出的三部分的面积进行相比即可.
解答:解:由题意知定义三个圆分别为小圆、中圆、大圆,
设小圆的半径是r,则中圆的半径为
r,大圆的半径为
r,
S小圆=
πr2,
S中圆=
π(
r)2=
πr2,
S大圆=
π(
r)2=
πr2,
A=C=
S大圆-
S中圆+
S小圆,
=
πr2-
πr2+
πr2,
=
πr2,
B=(
S中圆-
S小圆)×2,
=(
πr2-
πr2)×2,
=
πr2×2,
=
πr2,
所以:A:B:C=
πr2:
πr2:
πr2,
=2:1:2,
故答案为:2:1:2.
设小圆的半径是r,则中圆的半径为
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
A=C=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 25 |
| 8 |
| 9 |
| 8 |
| 1 |
| 2 |
=
| 5 |
| 2 |
B=(
| 1 |
| 2 |
| 1 |
| 2 |
=(
| 9 |
| 8 |
| 1 |
| 2 |
=
| 5 |
| 8 |
=
| 5 |
| 4 |
所以:A:B:C=
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
=2:1:2,
故答案为:2:1:2.
点评:此题要看清各部分面积是怎么来的,然后πr2整体运算,这两点很关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 某次射箭比赛中,所用的箭靶上画有4个同圆心的圆环.如图,每个圆环内的数字是射中此圆环时可得到的分数,运动员黄亮射中10支箭,每个圆环都有箭射中,共得110分,问:每个圆环各被射中几支?
某次射箭比赛中,所用的箭靶上画有4个同圆心的圆环.如图,每个圆环内的数字是射中此圆环时可得到的分数,运动员黄亮射中10支箭,每个圆环都有箭射中,共得110分,问:每个圆环各被射中几支?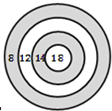 某次射箭比赛中,所用的箭靶上画有4个同心圆环,从外到内,分别标上8、12、14、18,如图,每个圆环内的数是射中此圆环时可得到的分数.运动员林得胜射中10支箭,每个圆环都有箭射中,共得110分.问:每个圆环各被射中几支箭?(在下面写出所有可能出现的情况的答案,分析过程可不写.)
某次射箭比赛中,所用的箭靶上画有4个同心圆环,从外到内,分别标上8、12、14、18,如图,每个圆环内的数是射中此圆环时可得到的分数.运动员林得胜射中10支箭,每个圆环都有箭射中,共得110分.问:每个圆环各被射中几支箭?(在下面写出所有可能出现的情况的答案,分析过程可不写.)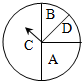 如图,旋转圆盘上的指针,指针落在A区域的可能性是
如图,旋转圆盘上的指针,指针落在A区域的可能性是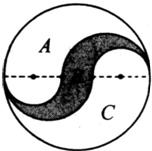 如图,大圆直径上的黑点是五等分点,则A、B、C三部分的面积比为________.
如图,大圆直径上的黑点是五等分点,则A、B、C三部分的面积比为________.