Question

如表，各行中的图案是由两种不同的图案按一定的规律演变，…，根据这样的规律，则在第8行中“☆”图案的个数是________．

第一行	☆
第二行			☆
第三行	☆			☆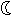
第四行		☆	☆		☆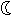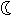
…	…

Answer 1

21
分析：观察图形可知，第一行有1个星，第二行有1个星，第三行有2个星，第四行有3个星，…，可以看出从第3行开始，星的个数是前面两个数字之和，由此即可解答．
解答：第一行有1个星，第二行有1个星，第三行有2个星，第四行有3个星，…，可以看出从第3行开始，星的个数是前面两个数字之和，
所以星星的个数依次可以排列为：1；1；2；3；5；8；13；21；
所以第8行中“☆”图案的个数是21．
故答案为：21．
点评：根据题干，找出星的个数排列特点，是解决本题的关键．