题目内容
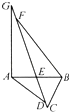
【题目】如图,点D、E、F在线段CG上,已知CD=2厘米,DE=8厘米,EF=20厘米,FG=4厘米,AB将整个图形分成上下两部分,下边部分面积是67平方厘米,上边部分面积是166平方厘米,则三角形ADG的面积是 平方厘米.
【答案】128
【解析】
试题分析:由图可知,S△ADE与S△AGE的高相等,是S△ADG的高,故设S△ADG的高为h1;同理可得,S△BCG的高为h2,利用等底等高的三角形面积相等可求结果.
解:设三角形ADE的高为h1,三角形BCE的高为h2,
则S△ADE+S△BCE=67;S△ACE+S△BFE=166,
即:24×h1+20×h2=166×2;
8×h1+10×h2=67×2,
解得:h1=8(厘米),
所以S△ADG=(8+20+4)×8÷2=128(平方厘米);
故答案为:128.

练习册系列答案
相关题目
