题目内容
一个等腰三角形,与顶角相邻的外角度数是130°,顶角与底角分别是多少度?它是什么样的三角形?
分析:先根据三角形的外角的定义,可以求出等腰三角形的顶角是180°-130°=50°,再利用三角形内角和定理和等腰三角形的两个底角相等的性质,即可得到结果.
解答:解:根据题干分析可得,顶角是:180°-130°=50°,
则底角是:(180°-50°)÷2,
=130°÷2,
=65°,
三个角都是锐角,所以这个三角形是锐角三角形.
答:顶角是50°,底角是65°,是锐角三角形.
则底角是:(180°-50°)÷2,
=130°÷2,
=65°,
三个角都是锐角,所以这个三角形是锐角三角形.
答:顶角是50°,底角是65°,是锐角三角形.
点评:此题主要考查了等腰三角形的性质与三角形内角与外角的关系,属于基础题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
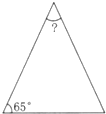 如图是一个等腰三角形.求顶角的度数.
如图是一个等腰三角形.求顶角的度数.