题目内容
一个正方形和一个圆的周长相等,它们的面积相比
- A.正方形的面积大
- B.圆的面积大
- C.相等
- D.无法比较
B
分析:周长相等的正方形和圆,圆的面积比正方形的面积大.可以通过举例证明,设周长是C,则正方形的边长是C÷4,圆的半径是C÷2π;根据它们的面积公式求出它们的面积,进行比较.
解答:设周长是c,则正方形的边长是 ,圆的半径是
,圆的半径是 ,
,
则圆的面积为: ×
× ×π=
×π=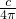 ×c=
×c=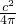 ;
;
正方形的面积为: ×
× =c2÷16=
=c2÷16= ,
,
则圆的面积:正方形的面积=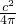 :
: =4:π.
=4:π.
所以圆的面积大.
故选:B.
点评:此题主要考查周长相等的正方形和圆,圆的面积比正方形的面积大.
分析:周长相等的正方形和圆,圆的面积比正方形的面积大.可以通过举例证明,设周长是C,则正方形的边长是C÷4,圆的半径是C÷2π;根据它们的面积公式求出它们的面积,进行比较.
解答:设周长是c,则正方形的边长是
 ,圆的半径是
,圆的半径是 ,
,则圆的面积为:
 ×
× ×π=
×π=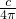 ×c=
×c=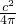 ;
;正方形的面积为:
 ×
× =c2÷16=
=c2÷16= ,
,则圆的面积:正方形的面积=
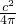 :
: =4:π.
=4:π.所以圆的面积大.
故选:B.
点评:此题主要考查周长相等的正方形和圆,圆的面积比正方形的面积大.

练习册系列答案
相关题目