题目内容
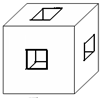 如图所示,在棱长为3的正方体中,由上到下,由左到右,由前到后的居中位置各钻一个洞,其洞口为一正方形,面积为1且洞深为3.求所得几何体的总表面积.
如图所示,在棱长为3的正方体中,由上到下,由左到右,由前到后的居中位置各钻一个洞,其洞口为一正方形,面积为1且洞深为3.求所得几何体的总表面积.分析:先算出正方体的表面积是3×3×6=54,然后因为表面打的有洞,所以应减去正方体表面的6个小正方形的面积得54-6×1=48,然后再算中间的洞的表面积,这三个洞在正方体中间有交叉连接,在正方体的中心的表面积为0,另外那个长方形的洞的底面积总共是6,在上一部中已经减去了,所以现在只要算的那三个长方体的表面积中就不要底面积,也就是说这三个长方体的表面积实际上是24个边长为1的正方形的表面积,得 24×1=24,最后的答案是 48+24=72.
解答:解:正方体的表面积:3×3×6=54,
去掉6个小正方形后的面积:54-6×1=48,
24个正方形的面积:24×1=24,
几何体的总表面积:48+24=72.
答:几何体的总表面积是72.
去掉6个小正方形后的面积:54-6×1=48,
24个正方形的面积:24×1=24,
几何体的总表面积:48+24=72.
答:几何体的总表面积是72.
点评:解答此题的关键是明白:三个洞的表面积的计算方法,24个正方形也可以说成是6个边长为1没有底面的正方体.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有55个棱长为1分米的正方体木块连体,在地面上摆成如图所示的形式,要在表面涂刷油漆,如果与地面接触的面不涂油漆,干后将小木块分开,则涂油漆的表面积与未涂油漆表面积的比是________.
有55个棱长为1分米的正方体木块连体,在地面上摆成如图所示的形式,要在表面涂刷油漆,如果与地面接触的面不涂油漆,干后将小木块分开,则涂油漆的表面积与未涂油漆表面积的比是________.
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … |
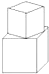 两个大小不同的正方体积木粘在一起,构成如图所示的立体图形,其中,小积木的粘贴面的四个顶点分别是大积木的粘贴面各边的一个三等分点.如果大积木的棱长为3,则这个立体图形的表面积为
两个大小不同的正方体积木粘在一起,构成如图所示的立体图形,其中,小积木的粘贴面的四个顶点分别是大积木的粘贴面各边的一个三等分点.如果大积木的棱长为3,则这个立体图形的表面积为
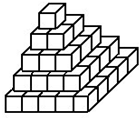 有55个棱长为1分米的正方体木块连体,在地面上摆成如图所示的形式,要在表面涂刷油漆,如果与地面接触的面不涂油漆,干后将小木块分开,则涂油漆的表面积与未涂油漆表面积的比是
有55个棱长为1分米的正方体木块连体,在地面上摆成如图所示的形式,要在表面涂刷油漆,如果与地面接触的面不涂油漆,干后将小木块分开,则涂油漆的表面积与未涂油漆表面积的比是