题目内容
20.两仓库一共有粮食240t,从甲仓库调走$\frac{3}{5}$,从乙仓库调走30t,两仓库粮食数量相等,乙仓库原有粮食多少吨?分析 设甲仓库原来有粮食x吨,乙仓库原来有240-x吨,从甲仓库调走$\frac{3}{5}$,还剩下1-$\frac{3}{5}=\frac{2}{5}$,还剩下$\frac{2}{5}x$吨,从乙仓库调走30吨,乙仓库还剩下240-x-30吨,这时两仓库粮食数量相等,也就是$\frac{2}{5}x$和240-x-30相等.据此解答.
解答 解:设甲仓库原来有粮食x吨,乙仓库原来有240-x吨.
(1-$\frac{3}{5}$)x=240-x-30
$\frac{2}{5}$x=240-x-30
$\frac{2}{5}x=210-x$
$\frac{2}{5}$x+x=210-x+x
1.4x=210
x=150
240-150=90(吨)
答:乙仓库原有粮食90吨.
点评 考查了复杂的分数应用题,用方程解答比较容易理解,本题的等量关系式是甲仓库和乙仓库剩下的重量相等.

练习册系列答案
相关题目
11.方程3.5x=0的解的情况是( )
| A. | 没有解 | B. | 有无数个解 | C. | 只有一个解 |
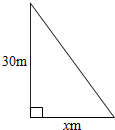 如图,一块直角三角形地的面积是150㎡,一条直角边的长是30m,另一条直角边的长是多少?
如图,一块直角三角形地的面积是150㎡,一条直角边的长是30m,另一条直角边的长是多少?