题目内容
在一个水池中有两根直立的木棍,木棍的一端紧贴着池底,另一端都露在水面上.两个木棍露出水面部分的长度之比是7:3.如果现在水池中的水面向上涨70厘米,这时两根木棍露出水面的部分的长度之比是7:2.那么原来这两根木棍露出水面部分的长度和是_____厘米?
- A.500
- B.490
- C.420
- D.370
A
分析:设两根木棍原来的露出水面部分的长度各是7x厘米和3x厘米,水池中的水面向上涨70厘米后,两根木棍的露出水面部分的长度各是7x-70厘米和3x-70厘米,再根据“这时两根木棍露出水面的部分的长度之比是7:2”,列出比例解答即可.
解答:设两根木棍原来的露出水面部分的长度各是7x厘米和3x厘米,
水池中的水面向上涨70厘米两根木棍的露出水面部分的长度各是7x-70厘米和3x-70厘米,
所以,(7x-70):(3x-70)=7:2,
(3x-70)×7=(7x-70)×2,
21x-490=14x-140,
7x=350,
x=350÷7,
x=50,
7x+3x=10x=10×50=500(厘米),
答:这两根木棍露出水面部分的长度和是500厘米;
故选:A.
点评:解答此题的关键是,根据题意设出未知量,找出对应量,列出比例解决问题.
分析:设两根木棍原来的露出水面部分的长度各是7x厘米和3x厘米,水池中的水面向上涨70厘米后,两根木棍的露出水面部分的长度各是7x-70厘米和3x-70厘米,再根据“这时两根木棍露出水面的部分的长度之比是7:2”,列出比例解答即可.
解答:设两根木棍原来的露出水面部分的长度各是7x厘米和3x厘米,
水池中的水面向上涨70厘米两根木棍的露出水面部分的长度各是7x-70厘米和3x-70厘米,
所以,(7x-70):(3x-70)=7:2,
(3x-70)×7=(7x-70)×2,
21x-490=14x-140,
7x=350,
x=350÷7,
x=50,
7x+3x=10x=10×50=500(厘米),
答:这两根木棍露出水面部分的长度和是500厘米;
故选:A.
点评:解答此题的关键是,根据题意设出未知量,找出对应量,列出比例解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
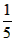 ,那么,水池中水深多少米?
,那么,水池中水深多少米?