题目内容
7.一项工程由甲、乙合做9天可以完成,若甲先独做8天后,再由乙独做12天可完工,问:这项工程由甲、乙单独做各要几天完工?分析 首先把这项工程看作单位“1”,根据工作效率=工作量÷工作时间,用1除以甲、乙合做需要的时间,求出甲、乙的工作效率之和是多少;然后判断出甲先独做8天后,再由乙独做12天,相当于甲、乙合做8天,再由乙单独做4(12-8=4)天,据此求出乙单独做4的工作量,进而求出乙的工作效率是多少;最后用甲乙的工作效率之和减去乙的工作效率,求出甲的工作效率是多少;再根据工作时间=工作量÷工作效率,分别用1除以甲乙的工作效率,求出这项工程由甲、乙单独做各要几天完工即可.
解答 解:1÷[(1-$\frac{1}{9}×8$)÷(12-8)]
=1÷[$\frac{1}{9}÷4$]
=1$÷\frac{1}{36}$
=36(天)
1÷($\frac{1}{9}-\frac{1}{36}$)
=1÷$\frac{1}{12}$
=12(天)
答:这项工程由甲单独做需要12天,由乙单独做需要36天.
点评 此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率,解答此题的关键是求出乙的工作效率是多少.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
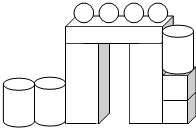 数一数,填一填.
数一数,填一填. 有3个,
有3个,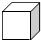 有2个,
有2个, 有3个,
有3个, 有4个;
有4个;