题目内容
有若干个相同的小正方体，组成一个大正方体，如果把大正方体的表面涂上红色，已知只有一面涂红色的小正方体有294个，则这个大正方体由________个小正方体组成．
729
分析：在大正方体的表面涂色，其中只有一面涂色的小正方体有294个，正方体有六个面，那么每个面都有294÷6=49个小正方体一面涂色，因为7×7=49，所以这个大正方体的每条棱长上有7+2=9个小正方体，由公式可以解决问题．
解答：每个面上一面涂色的有小正方体：294÷2=49（个），
因为7×7=49，
所以大正方体的每条棱长上有小正方体：7+2=9（个），
9×9×9=729（个），
答：这个大正方体由729个小正方体组成．
故答案为：729．
点评：一面涂色的小正方体都在大正方体的每个面上，此题的关键是根据“其中只有一面涂色的小正方体有6个”推理得出大正方体的棱长，由此解决问题．
分析：在大正方体的表面涂色，其中只有一面涂色的小正方体有294个，正方体有六个面，那么每个面都有294÷6=49个小正方体一面涂色，因为7×7=49，所以这个大正方体的每条棱长上有7+2=9个小正方体，由公式可以解决问题．
解答：每个面上一面涂色的有小正方体：294÷2=49（个），
因为7×7=49，
所以大正方体的每条棱长上有小正方体：7+2=9（个），
9×9×9=729（个），
答：这个大正方体由729个小正方体组成．
故答案为：729．
点评：一面涂色的小正方体都在大正方体的每个面上，此题的关键是根据“其中只有一面涂色的小正方体有6个”推理得出大正方体的棱长，由此解决问题．
练习册系列答案
相关题目
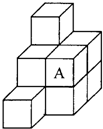把10个相同的小正方体按如图所示的位置堆放，它的外表含有若干个小正方形，如图将图中标有字母A的一个小正方体搬去，这时外表含有的小正方形个数与搬动前相比（ ）| A、不增不减 | B、减少1个 | C、减少2个 | D、减少3个 |