题目内容
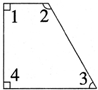
量出下面图形中各角的度数,你发现了什么?

∠1=
∠2=
∠3=
∠1+∠2+∠3=

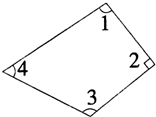
∠4=
∠5=
∠6=
∠4+∠5+∠6=
我发现:三角形的三个内角的度数之和为

∠1=
40°
40°
,∠2=
90°
90°
,∠3=
50°
50°
,∠1+∠2+∠3=
180°
180°
.
∠4=
70°
70°
,∠5=
50°
50°
,∠6=
60°
60°
,∠4+∠5+∠6=
50°
50°
.我发现:三角形的三个内角的度数之和为
180°
180°
.分析:先把量角器放在角的上面,使量角器的中心和角的顶点重合,零度刻度线和角的一条边重合,角的另一条边所对的量角器上的刻度,就是这个角的度数.可以发现:三角形的三个内角的度数之和为180°.
解答:解:经测量:∠1=40°,
∠2=90°,
∠3=50°,
∠1+∠2+∠3=40°+90°+50°=180°;
∠4=70°,
∠5=50°,
∠6=60°,
∠4+∠5+∠6=70°+50°+60°=180°.
故答案为:40°,90°,50°,180°;70°,50°,60°,180°.
∠2=90°,
∠3=50°,
∠1+∠2+∠3=40°+90°+50°=180°;
∠4=70°,
∠5=50°,
∠6=60°,
∠4+∠5+∠6=70°+50°+60°=180°.
故答案为:40°,90°,50°,180°;70°,50°,60°,180°.
点评:此题主要是考查根据角的度量方法正确量出各角度数,以及三角形的内角和等于180°的性质.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目