题目内容
 如图所示,在正六边形A周围画出6个同样的正六边形(阴影部分),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;….按这个方法继续画下去,当画完第9圈时,图中共有________个与A相同的正六边形.
如图所示,在正六边形A周围画出6个同样的正六边形(阴影部分),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;….按这个方法继续画下去,当画完第9圈时,图中共有________个与A相同的正六边形.
271
分析:根据题意可知:第一圈有6个,第二圈有12个,第三圈有18个…,由此可以总结出一个公式,求出各圈的个数,然后加在一起即可.
解答:由题意知:第一圈有6个,第二圈有12个,第三圈有18个…,那么第n圈就有6n个正六边形,
所以共有:1+6×1+6×2+6×3+…6×9,
=1+6×(1+2+3+…+9),
=1+6×45,
=1+270,
=271(个);
故答案为:271.
点评:此题关键是找出计算每一圈的公式,然后利用乘法的分配律的逆运算.
分析:根据题意可知:第一圈有6个,第二圈有12个,第三圈有18个…,由此可以总结出一个公式,求出各圈的个数,然后加在一起即可.
解答:由题意知:第一圈有6个,第二圈有12个,第三圈有18个…,那么第n圈就有6n个正六边形,
所以共有:1+6×1+6×2+6×3+…6×9,
=1+6×(1+2+3+…+9),
=1+6×45,
=1+270,
=271(个);
故答案为:271.
点评:此题关键是找出计算每一圈的公式,然后利用乘法的分配律的逆运算.

练习册系列答案
相关题目
 如图所示,在正六边形A周围画出6个同样的正六边形(阴影部分),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;….按这个方法继续画下去,当画完第9圈时,图中共有
如图所示,在正六边形A周围画出6个同样的正六边形(阴影部分),围成第1圈;在第1圈外面再画出12个同样的正六边形,围成第2圈;….按这个方法继续画下去,当画完第9圈时,图中共有 某地板厂要制作一批正六边形形状的地板砖,为适应市场多样化的需求,要求在地板砖上设计的图案能够把正六边形6等分,如图所示,请你再帮他们设计一些美观的等分方案(至少设计两种).
某地板厂要制作一批正六边形形状的地板砖,为适应市场多样化的需求,要求在地板砖上设计的图案能够把正六边形6等分,如图所示,请你再帮他们设计一些美观的等分方案(至少设计两种).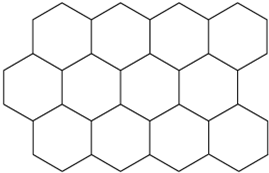 卡纸上编号1~4的图形均是由数量不等的相同大小的正六边形组成的.请完成以下问题:
卡纸上编号1~4的图形均是由数量不等的相同大小的正六边形组成的.请完成以下问题: 某地板厂要制作一批正六边形形状的地板砖,为适应市场多样化的需求,要求在地板砖上设计的图案能够把正六边形6等分,如图所示,请你再帮他们设计一些美观的等分方案(至少设计两种).
某地板厂要制作一批正六边形形状的地板砖,为适应市场多样化的需求,要求在地板砖上设计的图案能够把正六边形6等分,如图所示,请你再帮他们设计一些美观的等分方案(至少设计两种).