题目内容
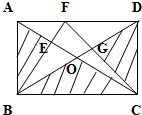如图，在长方形ABCD中，AD=20，AB=12，其中四边形OEFG的面积是30，请计算图中三块阴影部分的面积之和．
解：阴影部分面积：
×（20×12）+30，
=×240+30，
=120+30，
=150；
答：图中三块阴影部分的面积之和为150．
分析：由图意可知：S△CDF=S△DBF，同时减去公共部分三角形DFG，则剩下的面积还相等，即：S△FBG=S△CDG，于是阴影部分的面积就等于长方形的面积，再加四边形OEFG的面积，长方形的面积可求，四边形OEFG的面积已知，从而问题得解．
点评：解答此题的关键是：运用等量代换，将阴影部分的面积转化成和长方形的面积以及四边形OEFG的面积有关的图形的面积，于是可以求解．
×（20×12）+30，=
×240+30，=120+30，
=150；
答：图中三块阴影部分的面积之和为150．
分析：由图意可知：S△CDF=S△DBF，同时减去公共部分三角形DFG，则剩下的面积还相等，即：S△FBG=S△CDG，于是阴影部分的面积就等于
长方形的面积，再加四边形OEFG的面积，长方形的面积可求，四边形OEFG的面积已知，从而问题得解．点评：解答此题的关键是：运用等量代换，将阴影部分的面积转化成和长方形的面积以及四边形OEFG的面积有关的图形的面积，于是可以求解．
练习册系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
两个形状和大小都一样的直角三角形△ABC和△DEF，如图放置，它们的面积都是2003平方厘米，而每一个三角形的顶点恰好都落在另一个三角形的斜边上．这两个直角三角形的重叠部分是一个长方形，那么四边形ADEC的面积为
（2008?宝应县）（1）如表每小方格面积1平方厘米，先在图中画一个长4cm，宽3cm的长方形，再在长方形中画一个最大的圆，求出圆的面积．
（1）如表每小方格面积1平方厘米，先在图中画一个长4cm，宽3cm的长方形，再在长方形中画一个最大的圆，求出圆的面积．